ഗ്രൂപ്പ്

ഒരു ഗണവും ആ ഗണത്തിലെ ഏത് രണ്ട് അംഗങ്ങളെയും കൂട്ടിച്ചേർത്ത് അതേ ഗണത്തിലെ ഒരംഗത്തിനെത്തന്നെ തരുന്ന ദ്വയാങ്കസംക്രിയയും ചേർന്ന ബീജീയഘടനയെയാണ് ഗണിതത്തിൽ ഗ്രൂപ്പ് എന്ന് വിളിക്കുന്നത്. ഈ വിധത്തിൽ ഒരു ഗണവും സംക്രിയയും ചേർന്ന ജോഡി ഒരു ഗ്രൂപ്പ് ആകണമെങ്കിൽ, ഇവ ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങൾ എന്ന പേരുള്ള നാല് വ്യവസ്ഥകൾ അനുസരിക്കേണ്ടതുണ്ട്. സംവൃതിനിയമം, സാഹചര്യനിയമം, തൽസമകത്തിന്റെ അസ്തിത്വം, വിപരീതത്തിന്റെ അസ്തിത്വം എന്നിവയാണ് ഈ ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങൾ. പലതരം സംഖ്യാവ്യവസ്ഥകളുൾപ്പെടെ, ഗണിതത്തിലെ സുപരിചിതങ്ങളായ പല വ്യൂഹങ്ങളും ഈ സ്വയംപ്രമാണങ്ങൾ അനുസരിക്കുന്നു. പൂർണ്ണസംഖ്യകളുടെ ഗണവും സുപരിചിതമായ സങ്കലനം എന്ന സംക്രിയയും ചേർന്ന ബീജീയഘടന ഗ്രൂപ്പിന് ഉദാഹരണമാണ്. ഒരു പ്രത്യേക ഗണിതവ്യൂഹത്തെ മനസ്സിൽ കാണാതെ അമൂർത്തമായ രീതിയിൽ സ്വയംപ്രമാണങ്ങൾ നിർവചിച്ചിരിക്കുന്നതിനാൽ ബീജഗണിതത്തിലെയും ഗണിതത്തിലെ മറ്റ് ശാഖകളിലെയും നന്നേ വ്യത്യസ്തങ്ങളായ പലതരം ഗണിതരൂപങ്ങളെ അവയുടെ പ്രധാന ഘടനാഗുണങ്ങൾ നഷ്ടപ്പെടുത്താതെതന്നെ ഒരേപോലെ കൈകാര്യം ചെയ്യാൻ ഗ്രൂപ്പ് സിദ്ധാന്തത്തിന് സാധിക്കുന്നു. ഗണിതത്തിലും വിവിധ ശാസ്ത്രവിഷയങ്ങളിലും ഗ്രൂപ്പുകൾ പലയിടത്തും പ്രത്യക്ഷപ്പെടുന്നതിനാൽ ആധുനിക ഗണിതത്തിലെ കേന്ദ്ര ആശയങ്ങളിലൊന്നാണ് ഗ്രൂപ്പുകൾ.^[1]^[2]

സമമിതി എന്ന ആശയവുമായി ഗ്രൂപ്പുകൾക്ക് അടിസ്ഥാനപരമായ ബന്ധമുണ്ട്. ഒരു ജ്യാമിതീയവസ്തുവിന്റെ സമമിതികളെ അതിന്റെ സമമിതിഗ്രൂപ്പുപയോഗിച്ച് വിശദീകരിക്കാൻ സാധിക്കും : ഈ ഗ്രൂപ്പിലെ അംഗങ്ങൾ ജ്യാമിതീയവസ്തുവിന്റെ വ്യത്യാസമില്ലാതെ നിലനിർത്തുന്ന രൂപാന്തരണങ്ങളും സംക്രിയ രണ്ട് രൂപാന്തരണങ്ങളെ ഒന്നിനുപിന്നാലെ ഒന്നായി പ്രയോഗിക്കലുമാണ്. സമമിതിഗ്രൂപ്പുകളായ ലീ ഗ്രൂപ്പുകൾക്ക് കണികാഭൗതികത്തിലെ സ്റ്റാൻഡേർഡ് മോഡലിൽ ഉപയോഗമുണ്ട്. രസതന്ത്രത്തിൽ തന്മാത്രകളുടെ സമമിതി വിവരിക്കാൻ പോയിന്റ് ഗ്രൂപ്പുകൾ സഹായിക്കുന്നു. സാമാന്യ ആപേക്ഷികതയുടെ അടിസ്ഥാനപരമായ സമമിതി വിശദീകരിക്കുന്നത് പോങ്കാരെ ഗ്രൂപ്പുകളെ ഉപയോഗിച്ചാണ്.

ബഹുപദസമവാക്യങ്ങളെക്കുറിച്ചുള്ള പഠനങ്ങളിൽ നിന്നാണ് ഗ്രൂപ്പ് എന്ന ആശയം ഉരുത്തിരിഞ്ഞത്. 1830-കളിൽ ഇവാരിസ്റ്റെ ഗാൽവ ആണ് ഇതിന് തുടക്കം കുറിച്ചത്. ജ്യാമിതി, സംഖ്യാസിദ്ധാന്തം എന്നിവയുൾപ്പെടെയുള്ള മറ്റ് ഗണിതശാഖകളിൽ നിന്നുള്ള സംഭാവനകളോടെ വികസിച്ച ആശയം 1870 ആയപ്പോഴേക്ക് പൂർണ്ണത നേടി. ഗ്രൂപ്പുകളെ അമൂർത്തമായ രിതിയിൽ പഠിക്കുന്ന ഗ്രൂപ്പ് സിദ്ധാന്തം ഇന്ന് ഗണിതത്തിൽ കാര്യമായി ഗവേഷണം നടക്കുന്ന ശാഖയാണ്. ഗ്രൂപ്പുകളെ സമഗ്രമായി പഠിക്കുന്നതിൽ സഹായിക്കാനായി ഗണിതജ്ഞർ അവയെ ഉപഗ്രൂപ്പുകൾ, ഘടകഗ്രൂപ്പുകൾ, ലളിതഗ്രൂപ്പുകൾ എന്നിങ്ങനെ ചെറിയ കഷണങ്ങളാക്കി ഭാഗിക്കാനുള്ള രീതികളും കണ്ടെത്തിയിട്ടുണ്ട്. അമൂർത്തമായ സ്വഭാവസവിശേഷതകൾക്കുപുറമെ പ്രത്യേക ഗ്രൂപ്പുകളെ മൂർത്തമായി സൂചിപ്പിക്കുന്നതിന്റെ വിവിധ രീതികളെക്കുറിച്ച് പ്രാതിനിധ്യസിദ്ധാന്തം, കമ്പ്യൂട്ടേഷണൽ ഗ്രൂപ്പ് സിദ്ധാന്തം എന്നീ വിഷയങ്ങളിലും ഗവേഷണങ്ങൾ നടക്കുന്നു. പരിബദ്ധഗ്രൂപ്പുകളെ സംബന്ധിച്ച് പ്രത്യേകിച്ചും വളരെയധികം ഗവേഷണങ്ങൾ നടന്നിട്ടുള്ളതാണ്. ഇത് 1983-ൽ പരിബദ്ധ ലളിതഗ്രൂപ്പുകളുടെ വർഗ്ഗീകരണം കണ്ടുപിടിക്കുന്നതിലേക്ക് നയിച്ചു. ഇതിനുശേഷം 1980-കളുടെ മധ്യം മുതൽ ജ്യാമിതീയ ഗ്രൂപ്പ് സിദ്ധാന്തം ഗ്രൂപ്പ് സിദ്ധാന്തത്തിലെ വളരെ സക്രിയമായ ഒരു ശാഖയായിമാറിയിട്ടുണ്ട്.

ഫലകം:TOClimit

ഉദാഹരണങ്ങൾ

ആദ്യത്തെ ഉദാഹരണം : പൂർണ്ണസംഖ്യകൾ

ഏറ്റവും പരിചിതമായ ഗ്രൂപ്പുകളിലൊന്നാണ് പൂർണ്ണസംഖ്യാഗണമായ Z, ദ്വയാങ്കസംക്രിയയായ സങ്കലനം എന്നിവ ചേർന്ന ഗ്രൂപ്പ്.

..., −4, −3, −2, −1, 0, 1, 2, 3, 4, ...^[3] ആണ് ഈ ഗ്രൂപ്പിലെ അംഗങ്ങൾ.

പൂർണ്ണസംഖ്യകളുടെ താഴെപ്പറയുന്ന സവിശേഷതകൾ അമൂർത്തമായ ഗ്രൂപ്പ് സ്വയംപ്രമാണസിദ്ധാന്തങ്ങളുമായി ഒത്തുപോകുന്നു:

a, b എന്നിവ പൂർണ്ണസംഖ്യകളാണെങ്കിൽ അവയുടെ തുകയായ a + b യും ഒരു പൂർണ്ണസംഖ്യയായിരിക്കും. ഈ സ്വഭാവത്തെ സംവൃതി എന്ന് വിളിക്കുന്നു
a, b, c എന്ന ഏത് മൂന്ന് പൂർണ്ണസംഖ്യകൾക്കും (a + b) + c = a + (b + c) ആയിരിക്കും. അതായത്, a യും b യും തമ്മിൽ കൂട്ടിയാൽ കിട്ടുന്ന സംഖ്യയെ c യോടു കൂട്ടിയാലും, a യെ b യും c യും തമ്മിൽ കൂട്ടിയാൽ കിട്ടുന്ന സംഖ്യയോടു കൂട്ടിയാലും കിട്ടുന്ന ഫലം തുല്യമായിരിക്കും. ഇതിനെ സാഹചര്യനിയമം എന്ന് വിളിക്കുന്നു
a ഏതൊരു പൂർണ്ണസംഖ്യയാണെങ്കിലും 0 + a = a + 0 = a. അതായത് പൂജ്യത്തോട് ഏത് പൂർണ്ണസംഖ്യ കൂട്ടിയാലും ആ സംഖ്യ തന്നെ ലഭിക്കും. അതിനാൽ പൂജ്യത്തെ സങ്കലനത്തിന്റെ തൽസമകം എന്ന് വിളിക്കുന്നു
a ഒരു പൂർണ്ണസംഖ്യയാണെങ്കിൽ a + b = b + a = 0 ആകുന്ന തരത്തിൽ b എന്ന ഒരു പൂർണ്ണസംഖ്യ ഉണ്ടായിരിക്കും. b യെ a യുടെ സങ്കലനവിപരീതം എന്ന് വിളിക്കുകയും −a എന്ന ചിഹ്നം കൊണ്ട് സൂചിപ്പിക്കുകയും ചെയ്യുന്നു.

പൂർണ്ണസംഖ്യാഗണവും സങ്കലനസംക്രിയയും ചേർന്ന ബീജീയഘടന മറ്റനേകം ഗണിതവ്യൂഹങ്ങളുമായി ഘടനയിലും സ്വഭാവത്തിലും ഏറെ സാമ്യം പുലർത്തുന്നു. ഈ ഗണിതവ്യൂഹങ്ങളുടെയെല്ലാം സ്വഭാവങ്ങളെ ഒരുമിച്ച് വിശദീകരിക്കാനാണ് ഗ്രൂപ്പുകൾ എന്ന അമൂർത്തമായ ആശയം വികസിപ്പിച്ചെടുക്കുന്നത്. ഈ ആവശ്യത്തിലേക്കായി ഗ്രൂപ്പുകളെ ഇപ്രകാരം നിർവചിക്കാം:

ഗ്രൂപ്പ് : നിർവചനം

G എന്ന ഗണവും ഗണത്തിലെ ഏത് രണ്ട് അംഗങ്ങളെയും കൂട്ടിച്ചേർത്ത് അതേ ഗണത്തിലെ ഒരംഗത്തിനെത്തന്നെ തരുന്ന • എന്ന ദ്വയാങ്കസംക്രിയയും (ഇതിനെ G യുടെ ഗ്രൂപ്പ് നിയമം എന്നും വിളിക്കുന്നു) ചേർന്ന ഫലകം:Nowrap എന്ന ക്രമജോഡിയാണ് ഗ്രൂപ്പ്. ഗണത്തിലെ a, b എന്ന അംഗങ്ങളുടെമേൽ ദ്വയാങ്കസംക്രിയ പ്രയോഗിക്കുമ്പോൾ കിട്ടുന്ന ഫലത്തെ ഫലകം:Nowrap അഥവാ ab എന്ന് സൂചിപ്പിക്കുന്നു. ഫലകം:Nowrap എന്ന ക്രമജോഡി ഒരു ഗ്രൂപ്പാകണമെങ്കിൽ ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങൾ എന്നറിയപ്പെടുന്ന നാല് വ്യവസ്ഥകളനുസരിക്കേണ്ടതുണ്ട്:^[4]

സംവൃതിനിയമം: a, b എന്നിവ G യിലെ അംഗങ്ങളാണെങ്കിൽ a • b യും G യിലെ അംഗമായിരിക്കണം.
സാഹചര്യനിയമം: a, b, c എന്നിവ G യിലെ അംഗങ്ങളാണെങ്കിൽ (a • b) • c = a • (b • c) ആയിരിക്കണം.
തൽസമകത്തിന്റെ അസ്തിത്വം: a എന്നത് G യിലെ ഏതൊരംഗമാണെങ്കിലും ഫലകം:Nowrap begine • a = a • e = aഫലകം:Nowrap end എന്ന സമവാക്യം ശരിയായി വരുന്ന തരത്തിലുള്ള e എന്ന ഒരംഗം G യിൽ ഉണ്ടായിരിക്കണം. ഇത്തരം ഒരംഗമേ ഗ്രൂപ്പിലുണ്ടാകൂ എന്ന് തെളിയിക്കാനാകും, e യെ ഗ്രൂപ്പിന്റെ തൽസമകം എന്ന് വിളിക്കുന്നു
വിപരീതത്തിന്റെ അസ്തിത്വം: G യിലെ അംഗമായ ഓരോ a യ്ക്കും, a • b = b • a = e എന്ന സമവാക്യം ശരിയായി വരുന്ന തരത്തിൽ b എന്ന അംഗം G യിൽ ഉണ്ടായിരിക്കണം. b യെ a യുടെ വിപരീതം എന്ന് വിളിക്കുന്നു

a, b എന്നീ അംഗങ്ങളുടെമേൽ ദ്വയാങ്കസംക്രിയ പ്രയോഗിച്ചാൽ കിട്ടുന്ന ഫലം ക്രമത്തെ ആശ്രയിച്ചിരിക്കാം. അതായത്,

ഫലകം:Nowrap begina • b = b • aഫലകം:Nowrap end

എന്ന സമവാക്യം എല്ലായ്പോഴും ശരിയായിക്കൊള്ളണമെന്നില്ല. സങ്കലനം ക്രമനിയമമനുസരിക്കുന്നതിനാൽ ഈ സമവാക്യം പൂർണ്ണസംഖ്യകളുടെ സങ്കലനഗ്രൂപ്പിന്റെ കാര്യത്തിൽ എല്ലായ്പ്പോഴും ശരിയായിരിക്കും, എന്നാൽ താഴെ കൊടുത്തിരിക്കുന്ന ഡൈഹെഡ്രൽ ഗ്രൂപ്പിന്റെ കാര്യത്തിൽ അങ്ങനെയല്ല. ഫലകം:Nowrap begina • b = b • aഫലകം:Nowrap end എന്ന സമവാക്യമനുസരിക്കുന്ന ഗ്രൂപ്പുകളെ ക്രമഗ്രൂപ്പുകൾ എന്ന് വിളിക്കുന്നു.

ഗുണനരീതിയിൽ എഴുതുന്ന (അതായത്, ദ്വയാങ്കസംക്രിയയെ • അഥവാ * കൊണ്ട് സൂചിപ്പിക്കുന്ന) ഗ്രൂപ്പുകളുടെ തൽസമകത്തെ 1 അഥവാ 1_G^[5] എന്ന് സൂചിപ്പിക്കാറുണ്ട്. ഗുണനത്തിലെ തൽസമകം 1 ആയതിനാലാണിത്. ഗ്രൂപ്പുകളെ സങ്കലനരിതിയിൽ എഴുതുകയാണെങ്കിൽ (അതായത്, സംക്രിയയെ + കൊണ്ട് സൂചിപ്പിക്കുമ്പോൾ) തൽസമകത്തെ 0 എന്നും സൂചിപ്പിക്കാറുണ്ട്. id എന്നതും തൽസമകത്തെ പ്രതിനിധീകരിക്കാനുപയോഗിക്കുന്ന ചിഹ്നമാണ്.

ഗണവും സംക്രിയയും ചേർന്ന ക്രമജോഡിയായ ഫലകം:Nowrap ആണ് ഗ്രൂപ്പെങ്കിലും പലപ്പോഴും ഗ്രൂപ്പിലെ ഗണത്തിന്റെ ചിഹ്നമായ G ഗ്രൂപ്പിനെ പ്രതിനിധീകരിക്കാൻ ചുരുക്കരൂപമായി ഉപയോഗിക്കാറുണ്ട്. G എന്നത് ഗ്രൂപ്പിനെയാണോ അതോ ഗണത്തെയാണോ സൂചിപ്പിക്കുന്നത് എന്ന് സന്ദർഭത്തിൽ നിന്നും മനസ്സിലാക്കിയെടുക്കാൻ സാധിക്കും. ഉദാഹരണമായി, G യുടെ ഉപഗ്രൂപ്പാണ് H എന്ന് പറയുമ്പോൾ ഫലകം:Nowrap യുടെ ഉപഗ്രൂപ്പാണ് ഫലകം:Nowrap എന്നാണ് യഥാർത്ഥത്തിൽ ഉദ്ദേശിക്കുന്നത്.

രണ്ടാമത്തെ ഉദാഹരണം : ഒരു സമമിതിഗ്രൂപ്പ്

പരിക്രമണം, പ്രതിഫലനം എന്നിവ വഴി ഒരു ദ്വിമാനരൂപത്തെ മറ്റൊന്നാക്കി മാറ്റാൻ സാധിക്കുമെങ്കിൽ ആ ദ്വിമാനരൂപങ്ങൾ സർവ്വസമമാണെന്ന് പറയുന്നു. ഏതൊരു ദ്വിമാനരൂപവും അതിനോടുതന്നെ സർവ്വസമമാണ്. എന്നാൽ ചില രൂപങ്ങൾ തങ്ങളോട് ഒന്നിലേറെ രീതികളിൽ സർവ്വസമമായി വരുന്നു, ഈ സർവ്വസമതകളെ ദ്വിമാനരൂപത്തിന്റെ സമമിതികൾ എന്ന് വിളിക്കുന്നു. ഒരു സമചതുരത്തിന് എട്ട് സമമിതികളാണുള്ളത്:

id (തൽസമകം)	r₁ (ഘടികാരദിശയിൽ 90° പരിക്രമണം)	r₂ (ഘടികാരദിശയിൽ 180° പരിക്രമണം)	r₃ (ഘടികാരദിശയിൽ 270° പരിക്രമണം)
f_v (ലംബപ്രതിഫലനം)	f_h (തിരശ്ചീനപ്രതിഫലനം)	f_d (വികർണ്ണപ്രതിഫലനം)	f_c (വിപരീതവികർണ്ണപ്രതിഫലനം)
സമചതുരത്തിന്റെ സമമിതി ഗ്രൂപ്പായ (D₄) ലെ അംഗങ്ങൾ. ശീർഷങ്ങൾക്ക് നിറങ്ങളും സംഖ്യകളും നൽകിയിരിക്കുന്നത് തിരിച്ചറിയാൻ വേണ്ടിയാണ്

തൽസമകം : സമചതുരത്തെ വ്യത്യാസമില്ലാതെ നിലനിർത്തുക. id എന്ന് സൂചിപ്പിക്കുന്നു
പരിക്രമണം : സമചതുരത്തെ അതിന്റെ കേന്ദ്രത്തിനു ചുറ്റും ഘടികാരദിശയിൽ 90°, 180°, 270° പരിക്രമണം ചെയ്യുക. യഥാക്രമം r₁, r₂, r₃ എന്ന് സൂചിപ്പിക്കാം
പ്രതിഫലനം : സമചതുരത്തെ തിരശ്ചീനമായുള്ള മധ്യരേഖ, ലംബമായുള്ള മധ്യരേഖ, വിപരീതവികർണ്ണം, വികർണ്ണം എന്നിവയിലൂടെ പ്രതിഫലിപ്പിക്കുക. ഇവയെ യഥാക്രമം f_v, f_h, f_d, f_c എന്ന് സൂചിപ്പിക്കാം.

ഈ സമമിതികളെയെല്ലാം ഫലനങ്ങൾ കൊണ്ട് സൂചിപ്പിക്കാം. ഓരോ ഫലനവും സമചതുരത്തിലെ ഓരോ ബിന്ദുവിനെയും സമമിതിയനുസരിച്ചുള്ള പുതിയ സ്ഥാനത്തേക്ക് കൊണ്ടുപോകുന്നു. ഉദാഹരണമായി r₁ സമമിതിയെ കുറിക്കുന്ന ഫലനം ഓരോ ബിന്ദുവിനെയും സമചതുരത്തിന്റെ കേന്ദ്രത്തിനു ചുറ്റും 90°ഘടികാരദിശയിൽ പരിക്രമണം ചെയ്യിച്ചാലുള്ള സ്ഥാനത്തേക്കാണ് കൊണ്ടുപോവുക. രണ്ട് സമമിതികളെ സൂചിപ്പിക്കുന്ന ഫലനങ്ങളെ മിശ്രണം ചെയ്താൽ ലഭിക്കുന്ന ഫലനവും ഒരു സമമിതിയെ സൂചിപ്പിക്കുന്നതായിരിക്കും. സമചതുരത്തിന്റെ സമമിതികൾ ഒരു ഗ്രൂപ്പ് സൃഷ്ടിക്കുന്നു : ഡൈഹെഡ്രൽ ഗ്രൂപ്പായ D₄ ആണിത്. ഈ ഗ്രൂപ്പിന്റെ ഗണം മേല്പറഞ്ഞ സമമിതിഫലനങ്ങളുടെ ഗണവും ദ്വയാങ്കസംക്രിയ ഫലനമിശ്രണവുമാണ്.^[6] സമചതുരത്തിനുമേൽ a എന്ന സമമിതി പ്രയോഗിച്ച ശേഷം b എന്ന സമമിതി പ്രയോഗിക്കുന്നതിനെ ഇപ്രകാരമാണ് സൂചിപ്പിക്കുന്നത്:

ഫലകം:Nowrap beginb • aഫലകം:Nowrap end (a എന്ന സമമിതി പ്രയോഗിച്ച ശേഷം b എന്ന സമമിതി പ്രയോഗിക്കുക).

സമമിതിഫലനങ്ങൾ പ്രയോഗിക്കുന്ന ക്രമത്തിൽ വലത്തുനിന്ന് ഇടത്തോട്ടായി എഴുതുന്നത് സാധാരണ ഫലനമിശ്രണങ്ങളെ സൂചിപ്പിക്കുന്ന രീതിക്ക് സമാനമായാണ്.

വലതുഭാഗത്ത് നൽകിയിരിക്കുന്ന കെയ്ലി പട്ടിക ഇത്തരത്തിലുള്ള എല്ലാ ഫലനമിശ്രണങ്ങളെയും കാണിക്കുന്നു. ഉദാഹരണമായി, സമചതുരത്തെ 270° ഘടികാരദിശയിൽ പരിക്രമണം (r₃) ചെയ്യിച്ച ശേഷം തിരശ്ചീനപ്രതിഫലനം (f_h) ചെയ്യുന്നത് സമചതുരത്തെ വികർണ്ണപ്രതിഫലനം (f_d) ചെയ്യുന്നതിന് തുല്യമാണ്. ഈ മിശ്രണം പട്ടികയിൽ നീലനിറത്തിൽ കാണിച്ചിരിക്കുന്നു:

ഫലകം:Nowrap beginf_h • r₃ = f_d.ഫലകം:Nowrap end

D₄ ന്റെ കെയ്ലി പട്ടിക
•	id	r₁	r₂	r₃	f_v	f_h	f_d	f_c
id	id	r₁	r₂	r₃	f_v	f_h	f_d	f_c
r₁	r₁	r₂	r₃	id	f_c	f_d	f_v	f_h
r₂	r₂	r₃	id	r₁	f_h	f_v	f_c	f_d
r₃	r₃	id	r₁	r₂	f_d	f_c	f_h	f_v
f_v	f_v	f_d	f_h	f_c	id	r₂	r₁	r₃
f_h	f_h	f_c	f_v	f_d	r₂	id	r₃	r₁
f_d	f_d	f_h	f_c	f_v	r₃	r₁	id	r₂
f_c	f_c	f_v	f_d	f_h	r₁	r₃	r₂	id
id, r₁, r₂, and r₃ എന്നിവ ഒരു ഉപഗ്രൂപ്പ് സൃഷ്ടിക്കുന്നു, ഇത് ചുവപ്പുനിറത്തിൽ കാണിച്ചിരിക്കുന്നു. ഈ ഉപഗ്രൂപ്പിന്റെ ഒരു ഇടതുസഹഗണം പച്ചനിറത്തിലും ഒരു വലതുസഹഗണം മഞ്ഞനിറത്തിലും കാണിച്ചിരിക്കുന്നു

സമമിതികളുടെ ഗണവും സംക്രിയയായ ഫലനമിശ്രണവുമുപയോഗിച്ച് ഈ ഗ്രൂപ്പിൽ ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങൾ എപ്രകാരം അനുസരിക്കപ്പെടുന്നുവെന്ന് മനസ്സിലാക്കാം:

ഏത് രണ്ട് സമമിതികളുടെ മിശ്രണവും ഒരു സമമിതി തന്നെയായിരിക്കണമെന്നാണ് സംവൃതിനിയമം അനുശാസിക്കുന്നത്. അതായത്, a, b എന്നിവ സമമിതികളാണെങ്കിൽ ഫലകം:Nowrap beginb • aഫലകം:Nowrap end എന്നതും ഒരു സമമിതിയായിരിക്കണം. ഗ്രൂപ്പ് പട്ടികയിലെ അംഗങ്ങളെല്ലാം സമമിതികളാണ് എന്നതിൽ നിന്ന് ഈ ഗ്രൂപ്പ് സംവൃതിനിയമം അനുസരിക്കുന്നുവെന്ന് കാണാം
രണ്ടിൽക്കൂടുതൽ സമമിതികളെ മിശ്രണം ചെയ്യേണ്ടിവരുന്ന അവസരത്തിലാണ് സാഹചര്യനിയമം പ്രസക്തമാവുന്നത്. a, b, c എന്നിങ്ങനെ D₄ ലെ മൂന്ന് അംഗങ്ങളെടുക്കുകയാണെങ്കിൽ ഈ മൂന്ന് സമമിതികളെ ക്രമത്തിൽ മിശ്രണം ചെയ്ത് പുതിയൊരു സമമിതി നിർമ്മിക്കുന്നത് രണ്ട് വിധത്തിലാകാം : ആദ്യം a, b എന്നിവയെ മിശ്രണം ചെയ്ത് ഒറ്റ സമമിതിയാക്കി അതിനെ c യോട് മിശ്രണം ചെയ്യാം, അല്ലെങ്കിൽ ആദ്യം b, c എന്നിവയെ മിശ്രണം ചെയ്ത് a യെ ഈ സമമിതിയോട് മിശ്രണം ചെയ്യാം. ഈ രണ്ട് രീതികളും ഒരേ ഫലം നൽകുമെന്നാണ് സാഹചര്യനിയമം പറയുന്നത്.
ഫലകം:Nowrap begin(a • b) • c = a • (b • c)ഫലകം:Nowrap end
അതായത് കുറേ ഗ്രൂപ്പ് അംഗങ്ങളുടെ മിശ്രണഫലത്തെ ഏത് ക്രമത്തിലും ലഘൂകരിക്കാം. ഉദാഹരണമായി ഫലകം:Nowrap begin (f_d • f_v) • r₂ = f_d • (f_v • r₂)ഫലകം:Nowrap end എന്ന് ഗ്രൂപ്പ് പട്ടികയിൽ നിന്ന് കാണാൻ സാധിക്കും.

(f_d • f_v) • r₂ = r₃ • r₂ = r₁, ഇത്

f_d • (f_v • r₂) = f_d • f_h = r₁ എന്നതിന് തുല്യമാണ്.
സമചതുരത്തിന്റെ സമമിതികളും പൂർണ്ണസംഖ്യകളുടെ സങ്കലനവും സാഹചര്യനിയമം അനുസരിക്കുന്നുവെങ്കിലും എല്ലാ ദ്വയാങ്കസംക്രിയകളും ഇപ്രകാരമല്ല. വ്യവകലനം നല്ലൊരു ഉദാഹരണമാണ് : ഫലകം:Nowrap begin(7 − 3) − 2 = 2ഫലകം:Nowrap end ≠ ഫലകം:Nowrap begin7 − (3 − 2) = 6.ഫലകം:Nowrap end സാഹചര്യനിയമമനുസരിച്ച് ലഘൂകരണക്രമം ഏതുമാകാമെങ്കിലും മിശ്രണത്തിലെ അംഗങ്ങളുടെ ക്രമം തെറ്റാതെ നോക്കേണ്ടതാണ് - അതായത്, (a • b) • c, (b • a) • c എന്നിവയുടെ ഫലം തുല്യമായിക്കൊള്ളണമെന്നില്ല.
സമചതുരത്തെ വ്യത്യാസമില്ലാതെ നിലനിർത്തുന്ന id എന്ന സമമിതിയാണ് ഗ്രൂപ്പിലെ തൽസമകം. ഏതൊരംഗത്തിനും മുമ്പോ ശേഷമോ id പ്രയോഗിച്ചാൽ ആ അംഗം തന്നെ ലഭിക്കും. അതായത്,
ഫലകം:Nowrap beginid • a = a,ഫലകം:Nowrap end

ഫലകം:Nowrap begina • id = a.ഫലകം:Nowrap end
ഒരു അംഗം സമചതുരത്തിൽ വരുത്തുന്ന മാറ്റങ്ങൾ തിരസ്കരിക്കുന്ന അംഗത്തെയാണ് അതിന്റെ വിപരിതം എന്ന് വിളിക്കുന്നത്. സമചതുരത്തിന്റെ മേൽ ഏതൊരു സമമിതി പ്രയോഗിക്കുകയാണെങ്കിലും ഫലങ്ങൾ മറ്റൊരു സമമിതി ഉപയോഗിച്ച് തിരസ്കരിക്കാൻ സാധിക്കും. തൽസമകമായ id, പ്രതിഫലനങ്ങളായ f_h, f_v, f_d, f_c, 180° പരിക്രമണമായ r₂ എന്നിവ അവയുടെ തന്നെ വിപരീതങ്ങളാണ്. അതായത്, ഇവയിൽ ഏതെങ്കിലും ഒരു സമമിതി രണ്ടു തവണ പ്രയോഗിച്ചാൽ സമചതുരം ആദ്യമുണ്ടായിരുന്ന അവസ്ഥയിൽ തന്നെ തിരിച്ചെത്തും. പരിക്രമണങ്ങളായ r₃, r₁ എന്നിവ പരസ്പരം വിപരീതങ്ങളാണ് - കാരണം, സമചതുരത്തെ 90° പരിക്രമണം ചെയ്ത ശേഷം 270° (അഥവാ വിപരീതക്രമത്തിൽ) പരിക്രമണം ചെയ്താൽ സമചതുരം ആകെ 360° ഡിഗ്രി പരിക്രമണം ചെയ്യപ്പെടുകയും പൂർവ്വാവസ്ഥയിൽ തിരിച്ചെത്തുകയും ചെയ്യുന്നു. അതായത്,
ഫലകം:Nowrap beginf_h • f_h = id,ഫലകം:Nowrap end

ഫലകം:Nowrap beginr₃ • r₁ = r₁ • r₃ = id.ഫലകം:Nowrap end

പൂർണ്ണസംഖ്യാഗണത്തിൽ സങ്കലനം ചെയ്യുമ്പോൾ കിട്ടുന്ന ഫലം സംഖ്യകളുടെ ക്രമത്തെ ആശ്രയിച്ചിരുന്നില്ലെങ്കിലും D₄ൽ സ്ഥിതി വ്യത്യസ്തമാണ്. ഫലകം:Nowrap beginf_h • r₁ = f_cഫലകം:Nowrap end, എന്നാൽ ഫലകം:Nowrap beginr₁ • f_h = f_d.ഫലകം:Nowrap end അതായത് D₄ ഒരു ക്രമഗ്രൂപ്പല്ല. ഗ്രൂപ്പിന്റെ കെയ്ലി പട്ടിക സമമിതീയമല്ലാത്തത് ഇതിനാലാണ്.

ചരിത്രം

ഗ്രൂപ്പ് എന്ന അമൂർത്തമായ ആശയം ഉരുത്തിരിഞ്ഞത് ഗണിതത്തിലെ വിവിധ ശാഖകളിൽ നിന്നുള്ള ആശയങ്ങളുടെ സമ്മേളനമായാണ്.^[7]^[8]^[9] നാലിൽ കൂടുതൽ കൃതിയുള്ള ബഹുപദസമവാക്യങ്ങൾക്ക് പൊതുവായുള്ള നിർധാരണം കണ്ടെത്താനുള്ള ശ്രമങ്ങളാണ് ഗ്രൂപ്പ് സിദ്ധാന്തത്തിന്റെ ആദ്യകാലപ്രചോദനമായത്. പൗളോ റഫ്ഫിനി, ജോസഫ്-ലൂയി ലഗ്രാഞ്ജ് എന്നിവരുടെ സംഭാവനകൾ വിപുലീകരിച്ച പത്തൊമ്പതാം നൂറ്റാണ്ടിലെ ഫ്രഞ്ച് ഗണിതശാസ്ത്രജ്ഞനായ ഇവാരിസ്റ്റെ ഗാൽവ ബഹുപദസമവാക്യങ്ങളുടെ മൂലങ്ങളുടെ സമമിതിഗ്രൂപ്പ് ഉപയോഗിച്ച് ബഹുപദസമവാക്യം നിർധരിക്കുന്നത് സാധ്യമാകാനുള്ള നിബന്ധനകൾ കണ്ടുപിടിച്ചു. ഈ ഗാൽവ ഗ്രൂപ്പിലെ അംഗങ്ങൾ സമവാക്യത്തിന്റെ ചില മൂലങ്ങളുടെ ക്രമചയങ്ങളാണ്. ഗാൽവ ജീവിച്ചിരുന്ന കാലത്ത് അദ്ദേഹത്തിന്റെ ആശയങ്ങൾ മറ്റ് ഗണിതശാസ്ത്രജ്ഞർ തള്ളിക്കളഞ്ഞതിനാൽ അദ്ദേഹത്തിന്റെ മരണശേഷമാണ് അവ പ്രസിദ്ധീകരിച്ചത്.^[10]^[11] അഗസ്റ്റിൻ ലൂയി കൗച്ചി ക്രമചയഗ്രൂപ്പുകളെക്കുറിച്ച് കൂടുതൽ പഠിച്ചു. ആർതർ കെയ്ലിയുടെ 1854-ൽ പ്രസിദ്ധീകരിച്ച On the theory of groups, as depending on the symbolic equation θⁿ = 1 ആണ് പരിബദ്ധഗ്രൂപ്പുകളുടെ ആദ്യത്തെ അമൂർത്തനിർവചനം നൽകിയത്.^[12]

ഗ്രൂപ്പുകൾ വ്യാപകമായി ഉപയോഗിക്കപ്പെട്ട മറ്റൊരു ശാഖ ജ്യാമിതി ആയിരുന്നു. സമമിതിഗ്രൂപ്പുകൾ ജർമ്മൻ ഗണിതശാസ്ത്രജ്ഞനായ ഫെലിക്സ് ക്ലൈന്റെ എർലാങ്ങൻ പദ്ധതിയുടെ ഭാഗമായിരുന്നു.^[13] അതിവലയജ്യാമിതി, പ്രക്ഷേപജ്യാമിതി മുതലായ നവീന ജ്യാമിതികളുടെ ആവിർഭാവത്തിനുശേഷം ഗ്രൂപ്പ് സിദ്ധാന്തമുപയോഗിച്ച് വിവിധ ജ്യാമിതികളെ വർഗ്ഗീകരിക്കാനാണ് ക്ലൈൻ ശ്രമിച്ചത്. ഈ ആശയങ്ങളെ തുടർന്ന് വിപുലീകരിച്ച സോഫസ് ലീ ലീ ഗ്രൂപ്പുകളുടെ പഠനത്തിന് തുടക്കം കുറിച്ചു.^[14]

സംഖ്യാസിദ്ധാന്തവും ഗ്രൂപ്പ് ആശയങ്ങളുടെ നിർമ്മാണത്തിന് സംഭാവനകൾ നൽകി. ക്രമഗ്രൂപ്പുകളുടെ ചില സവിശേഷതകൾ കാൾ ഫ്രെഡറിക് ഗോസ്സ് 1798-ൽ പ്രസിദ്ധീകരിച്ച Disquisitiones Arithmeticae എന്ന സംഖ്യാസിദ്ധാന്തഗ്രന്ഥത്തിൽ അസ്പഷ്ടമായും പിന്നീട് ല്യോപോൾഡ് ക്രോണെക്കർ സ്പഷ്ടമായിത്തന്നെയും ഉപയോഗിച്ചു.^[15] 1847-ൽ ഫെർ‌മയുടെ അവസാന സിദ്ധാന്തം തെളിയിക്കാൻ ശ്രമിച്ച ഏൺസ്റ്റ് കുമ്മർ സംഖ്യകളെ അഭാജ്യസംഖ്യാഘടകങ്ങളായി ഘടകീകരിക്കുന്നത് വിശദീകരിക്കുന്ന ക്ലാസ് ഗ്രൂപ്പുകൾ ഉപയോഗിച്ചു.^[16]

വിവിധ ശാഖകളിൽ നിന്നുള്ള ഈ ആശയങ്ങളെ ഗ്രൂപ്പ് സിദ്ധാന്തം എന്ന ഗണിതശാഖയാക്കി ഒരുമിച്ചുചേർക്കുന്നത് ആരംഭിച്ചത് കാമിൽ ജോർഡാൻ 1870-ൽ എഴുതിയ Traité des substitutions et des équations algébriques എന്ന ഗ്രന്ധത്തോടെയാണ്.^[17] 1870-ൽ വാൽത്തെർ ഫോൺ ഡിക്ക് അമൂർത്തഗ്രൂപ്പുകൾക്ക് ആദ്യമായി ആധുനിക നിർവചനം നൽകി.^[18] പരിബദ്ധഗ്രൂപ്പുകളുടെ പ്രാതിനിധ്യസിദ്ധാന്തത്തെക്കുറിച്ചുള്ള പഠനങ്ങൾ നടത്തിയ ഫെർഡിനാൻഡ് ജോർജ് ഫ്രോബീനിയസ്, വില്യം ബേൺസൈഡ് എന്നിവരും റിച്ചാർഡ് ബ്രോവർ, ഐസക് ഷൂർ എന്നിവരുടെ പഠനങ്ങളും ഇരുപതാം നൂറ്റാണ്ടോടെ ഗ്രൂപ്പുകൾക്ക് ഗണിതശാസ്ത്രജ്ഞരുടെ ഇടയിൽ പൊതുസമ്മിതി നേടുന്നതിൽ സഹായിച്ചു.^[19] ഹെർമൻ വെയ്ൽ, ഏലീ കാർട്ടൻ ഉൾപ്പെടെയുള്ളവർ ലീ ഗ്രൂപ്പ് സിദ്ധാന്തം വിപുലീകരിച്ചു.^[20] ലീ ഗ്രൂപ്പുകളുടെ ബീജഗണിതത്തിലെ ഇരട്ടയായ ബീജീയഗ്രൂപ്പുകളുടെ പഠനം 1930-കളിൽ ക്ലോഡ് ഷെവാലെ തുടങ്ങിവെക്കുകയും അർമാൻഡ് ബോറെൽ, ഴാക് റ്റിറ്റ്സ് എന്നിവർ അത് മുന്നോട്ടുകൊണ്ടുപോവുകയും ചെയ്തു.^[21]

ഷിക്കാഗോ സർവകലാശാലയുടെ 1960-61 ലെ ഗ്രൂപ്പ് സിദ്ധാന്ത വർഷാചരണത്തിന്റെ ഭാഗമായി ഡാനിയൽ ഗോറൻസ്റ്റൈൻ, ജോൺ ജി. തൊംപ്സൺ, വാൾട്ടർ ഫെയ്റ്റ് ഉൾപ്പെടെയുള്ള ഗ്രൂപ്പ് സിദ്ധാന്തജ്ഞർ ഒരുമിച്ചു. ഇവരുടെ കൂട്ടായ്മയാണ് മറ്റനേകം ഗണിതജ്ഞരുടെ സഹായത്തോടെ 1982-ൽ എല്ലാ പരിബദ്ധ ലളിതഗ്രൂപ്പുകളുടെയും വർഗ്ഗീകരണം സാധിച്ചെടുത്തത്. വർഗ്ഗീകരണത്തിന്റെ തെളിവിന്റെ വലിപ്പത്തിന്റെ കാര്യത്തിലും ഇത് തെളിയിക്കുന്നതിൽ ഭാഗഭാക്കായ ഗവേഷകരുടെ എണ്ണത്തിന്റെ കാര്യത്തിലും ഈ പദ്ധതി അതുവരെ തെളിയിക്കപ്പെട്ടിരുന്ന എല്ലാ ഗണിതസിദ്ധാന്തങ്ങളെയും കവച്ചുവെച്ചു. ഈ വർഗ്ഗീകരണത്തിന്റെ തെളിവ് ലളിതവൽകരിക്കാനുള്ള ശ്രമങ്ങൾ ഇപ്പോഴും നടന്നുകൊണ്ടിരിക്കുകയാണ്.^[22] മറ്റനേകം ശാസ്ത്ര, ഗണിതശാസ്ത്ര ശാഖകളെ സ്വാധീനിക്കുന്ന ഗ്രൂപ്പ് സിദ്ധാന്തം ഇന്നും ഏറെ ഗവേഷണങ്ങൾ നടക്കുന്ന വിഷയമാണ്.

പ്രാഥമിക ഗ്രൂപ്പ് സിദ്ധാന്തം

ഗ്രൂപ്പുകളെക്കുറിച്ച് ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങളിൽ നിന്ന് നേരിട്ട് കണ്ടെത്താനാകുന്ന സവിശേഷതകളുടെ ശേഖരമാണ് പ്രാഥമിക ഗ്രൂപ്പ് സിദ്ധാന്തം.^[23] ഉദാഹരണമായി, സാഹചര്യനിയമം വീണ്ടും വീണ്ടും ഉപയോഗിക്കുകവഴി മൂന്നിലേറെ അംഗങ്ങളുടെ മേൽ സംക്രിയ പ്രയോഗിച്ചാലുള്ള ഫലം കാണുന്നത് ഏത് ക്രമത്തിൽ വേണമെങ്കിലും ആകാം എന്ന് മനസ്സിലാക്കാം. അതായത്

a • b • c = (a • b) • c = a • (b • c)

എന്നതുപോലെ മൂന്നിൽ കൂടുതൽ അംഗങ്ങളുള്ളപ്പോഴും കോഷ്ഠകങ്ങൾ ഏത് ക്രമത്തിലും ഇടാം. അതിനാൽ കോഷ്ഠകങ്ങൾ ഒഴിവാക്കാറാണ് പതിവ്.^[24]

ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങളെ ദുർബലപ്പെടുത്തി ഇടത് തൽസമകത്തിന്റെയും ഇടത് വിപരീതത്തിന്റെയും മാത്രം അസ്തിത്വം ആവശ്യപ്പെടാം. ഈ സ്വയംപ്രമാണങ്ങൾ ഉപയോഗിച്ചാൽ വലത് തൽസമകമുണ്ടെന്നും അത് ഇടത് തൽസമകത്തിന് തുല്യമാണെന്നും അതുപോലെ ഓരോ അംഗത്തിനും വലത് വിപരിതമുണ്ടെന്നും അത് ഇടത് വിപരീതത്തിന് ലഭ്യമാണെന്നും ലഭിക്കുന്നു. അതായത്, ഈ വിധത്തിൽ ദുർബലപ്പെടുത്തിയ ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങൾ പൂർണ്ണമായ ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങൾക്ക് തുല്യമാണ്.^[25]

തൽസമകവും വിപരിതങ്ങളും അദ്വിതീയമാണ്

തൽസമകവും വിപരീതങ്ങളും അദ്വിതീയമാണ് എന്നുള്ളത് ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങളുടെ അനന്തരഫലമാണ്. അതായത്, ഗ്രൂപ്പിൽ ഒരു തൽസമക അംഗമേ ഉണ്ടാകൂ. ഒരോ അംഗത്തിനും ഒരു വിപരീതം മാത്രമേ ഉണ്ടാകൂ താനും.^[26]

(G, •) എന്ന ഗ്രൂപ്പിൽ a എന്ന അംഗത്തിന്റെ വിപരീതം അദ്വിതീയമാണെന്ന് ഇപ്രകാരം തെളിയിക്കാം. a യ്ക്ക് b, c എന്ന രണ്ട് വിപരീതങ്ങളുണ്ടെന്ന് കരുതുക. എങ്കിൽ

b	=	b • e	e തൽസമകമായതിനാൽ
	=	b • (a • c)	c എന്നത് a യുടെ വിപരിതമായതിനാൽ e = a • c
	=	(b • a) • c	സാഹചര്യനിയമമുപയോഗിച്ച് കോഷ്ഠകങ്ങളുടെ സ്ഥാനം മാറ്റാം
	=	e • c	b യും a യുടെ വിപരിതമായതിനാൽ b • a = e
	=	c	e തൽസമകമായതിനാൽ

അതായത്, a യുടെ വിപരീതങ്ങളായ b യും c യും തുല്യമാണെന്നു വരുന്നു - a യുടെ വിപരിതം അദ്വിതീയമാണ്. ഇതുപോലെത്തന്നെ ഗ്രൂപ്പിന്റെ തൽസമകവും അദ്വിതീയമാണെന്ന് തെളിയിക്കാം. G എന്ന ഗ്രൂപ്പിന് e, f എന്നീ രണ്ട് തൽസമകങ്ങളുണ്ടെന്ന് കരുതുക. എങ്കിൽ e = e • f = f എന്ന് വരുന്നു, അതായത്, e യും f ഉം തുല്യമാണ്.

ഹരണം

ഗ്രൂപ്പുകൾ ഗുണനരീതിയിൽ എഴുതുകയാണെങ്കിൽ അംഗങ്ങളെ ഹരിക്കാൻ സാധിക്കുന്നതാണ്. a, b എന്നിവ G എന്ന ഗ്രൂപ്പിലെ അംഗങ്ങളാണെങ്കിൽ ഫലകം:Nowrap beginx • a = bഫലകം:Nowrap end എന്ന സമവാക്യം ശരിയാകുന്ന വിധത്തിൽ x എന്ന ഒറ്റ അംഗം മാത്രമേ G യിൽ ഉണ്ടാകൂ.^[26] സമവാക്യത്തെ വലതുഭാഗത്ത് a⁻¹ കൊണ്ട് ഗുണിച്ചാൽ ഈ അംഗം ലഭിക്കുന്നതാണ് : ഫലകം:Nowrap beginx = x • a • a⁻¹ = b • a⁻¹ഫലകം:Nowrap end. ഇതുപോലെ ഫലകം:Nowrap begina • y = bഫലകം:Nowrap end എന്ന സമവാക്യത്തിനും ഫലകം:Nowrap beginy = a⁻¹ • bഫലകം:Nowrap end എന്ന ഒറ്റ നിർദ്ധാരണം മാത്രമേ ഉണ്ടാകൂ. ഇവിടെ x, y എന്നിവ തുല്യമായിക്കൊള്ളണമെന്നില്ല.

g എന്ന ഗ്രൂപ്പ് അംഗത്തെക്കൊണ്ട് ഗുണിക്കുന്നത് ഒരു ഉഭയക്ഷേപഫലനമാണെന്നതാണ് ഇതിന്റെ പരിണതഫലം. G യിലെ ഒരംഗമാണ് g എങ്കിൽ h ∈ G യെ g • h ലേക്ക് കൊണ്ടുപോകുന്ന, G യിൽ നിന്ന് അതിലേക്കുതന്നെയുള്ള ഉഭയക്ഷേപഫലനമാണ് left translation. അതുപോലെ h നെ h • g ലേക്കു കൊണ്ടുപോകുന്ന ഉഭയക്ഷേപഫലനമാണ് right translation. G ഒരു ക്രമഗ്രൂപ്പാണെന്നുണ്ടെങ്കിൽ ഈ രണ്ട് ഫലനങ്ങളും തുല്യമാണ്.

അടിസ്ഥാന ആശയങ്ങൾ

തുടർന്നുവരുന്ന വിഭാഗങ്ങളിൽ X = {x, y, z} എന്നത് x, y, z എന്നീ അംഗങ്ങളടങ്ങിയ X എന്ന ഗണത്തെ സൂചിപ്പിക്കുന്നു. x ∈ X എന്ന് സൂചിപ്പിച്ചാൽ x എന്നത് X ലെ അംഗമാണെന്നാണ് ഉദ്ദേശ്യം. ഫലകം:Nowrap എന്നത് X ലെ ഓരോ അംഗത്തെയും Y ലെ ഏതെങ്കിലുമൊരു അംഗത്തിലേക്ക് കൊണ്ടുപോകുന്ന f എന്ന ഫലനത്തെ സൂചിപ്പിക്കുന്നു.

മേലെ കൊടുത്തിരിക്കുന്ന പ്രാഥമിക ഫലങ്ങളിൽ നിന്നും മുന്നോട്ടുപോകണമെങ്കിൽ ഗ്രൂപ്പിന്റെ ഘടനയെക്കുറിക്കുന്ന കൂടുതൽ ആശയങ്ങളുപയോഗിക്കേണ്ടതുണ്ട്. ഗ്രൂപ്പിൽ നാം ചേർക്കുന്ന ഏതൊരു ഘടനയും ഒരു തരത്തിൽ ഗ്രൂപ്പ് സംകാരകവുമായി ഒത്തുപോകുന്നതും ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങളനുസരിക്കുന്നതുമായിരിക്കണം. ഇത് നാം സൃഷ്ടിക്കുന്ന ഘടനകളുടെമേൽ നിബന്ധനകൾ നീർക്കുന്നു. ഉദാഹരണമായി, ഗ്രൂപ്പുകളെ തമ്മിൽ ഗ്രൂപ്പ് സമാംഗരൂപതകൾ എന്ന് വിളിക്കുന്ന ഫലനങ്ങൾ വഴി ബന്ധിപ്പിക്കാവുന്നതാണ്. എന്നാൽ ഇത്തരം ഫലനങ്ങൾ കൃത്യമായ രീതിയിൽ ഗ്രൂപ്പ് ഘടനയുമായി ഒത്തുപോകേണ്ടതുണ്ട്. ഗ്രൂപ്പ് ഘടനയെക്കുറിച്ച് കൂടുതൽ മനസ്സിലാക്കാനുള്ള മറ്റൊരു വഴി ഗ്രൂപ്പുകളെ ഉപഗ്രൂപ്പുകൾ, ഘടകഗ്രൂപ്പുകൾ എന്നിങ്ങനെ ചെറിയ കഷണങ്ങളായി വിഭജിക്കുക എന്നതാണ്.

ഗ്രൂപ്പ് സമാംഗരൂപത

ഫലകം:Main ഗ്രൂപ്പിന്റെ ഘടന നിലനിർത്തുന്ന ഫലനങ്ങളാണ് ഗ്രൂപ്പ് സമാംഗരുപതകൾ. (G,•) എന്ന ഗ്രൂപ്പിൽ നിന്ന് (H,*) എന്ന ഗ്രൂപ്പിലേക്കുള്ള ഫലകം:Nowrap begina: G → Hഫലകം:Nowrap end എന്ന ഫലനം ഒരു സമാംഗരൂപതയാകാനുള്ള നിബന്ധന g, k എന്നിവ G യിലെ അംഗങ്ങളാണ് എന്നുണ്ടെങ്കിൽ

ഫലകം:Nowrap begina(g • k) = a(g) * a(k)ഫലകം:Nowrap end

എന്ന സമവാക്യം അനുസരിക്കലാണ്. അതായത്, ഗ്രൂപ്പ് സംക്രിയ ഫലനം പ്രയോഗിക്കുന്നതിന് മുമ്പ് ചെയ്താലും ശേഷം ചെയ്താലും ഫലം തുല്യമായിരിക്കണം. ഈ നിബന്ധനയുടെ ഫലമായി ഫലകം:Nowrap begina(1_G) = 1_Hഫലകം:Nowrap end എന്നും, g എന്നത് G യിലെ ഏതൊരു അംഗമായാലും ഫലകം:Nowrap begina(g)⁻¹ = a(g⁻¹)ഫലകം:Nowrap end എന്നും ലഭിക്കുന്നു. അതായത്, ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങൾ G യിൽ അടിച്ചേൽപിക്കുന്ന ഘടനയോട് ഗ്രൂപ്പ് സമാംഗരൂപതയും ഒത്തുപോകുന്നു.^[27]

ഒന്നിനുപിറകെ ഒന്നായി ഫലകം:Nowrap begina: G → Hഫലകം:Nowrap end, ഫലകം:Nowrap beginb: H → Gഫലകം:Nowrap end എന്നിവ പ്രയോഗിക്കുകവഴി G, H എന്നീ ഗ്രൂപ്പുകളുടെ തൽസമകഫലനം ലഭിക്കുന്ന തരത്തിൽ a, b എന്ന ഗ്രൂപ്പ് സമാംഗരൂപതകൾ നിർവചിക്കാമെങ്കിൽ ഗ്രൂപ്പുകൾ സമരൂപമാണെന്ന് പറയുന്നു. അതായത്, G യിലെ ഏത് g യ്ക്കും H ലെ ഏത് h നും ഫലകം:Nowrap begina(b(h)) = hഫലകം:Nowrap end, ഫലകം:Nowrap beginb(a(g)) = gഫലകം:Nowrap end എന്നിങ്ങനെ ആയിരിക്കണം. ഗ്രൂപ്പ് സിദ്ധാന്തത്തിന്റെ വീക്ഷണകോണിൽ സമരൂപമായ ഗ്രൂപ്പുകൾ തുല്യമാണ്. ഉദാഹരണമായി G എന്ന ഏതെങ്കിലും ഗ്രൂപ്പിലെ അംഗമായ g യ്ക്ക് ഫലകം:Nowrap beging • g = 1_Gഫലകം:Nowrap end എന്ന സമവാക്യം ശരിയാണ് എന്ന് തെളിയിക്കുന്നത് ഫലകം:Nowrap begina(g) * a(g) = 1_H,ഫലകം:Nowrap end എന്ന് തെളിയിക്കുന്നതിന് തുല്യമാണ്. കാരണം, ഒന്നാമത്തെ സമവാക്യത്തിൽ a പ്രയോഗിച്ചാൽ രണ്ടാമത്തേതും രണ്ടാമത്തെ സമവാക്യത്തിൽ b പ്രയോഗിച്ചാൽ ആദ്യത്തെ സമവാക്യവും ലഭിക്കുന്നു.

ഉപഗ്രൂപ്പ്

ഫലകം:Main

ഒരു ഗ്രൂപ്പിൽ ഉൾക്കൊണ്ടിരിക്കുന്ന ചെറിയ ഗ്രൂപ്പിനെയാണ് ഉപഗ്രൂപ്പ് എന്ന് വിളിക്കുന്നത്.^[28] ഒരു ഗ്രൂപ്പിന്റെ ഗണത്തിന്റെ ഉപഗണം ആ ഗ്രൂപ്പിന്റെ ദ്വയാങ്കസംക്രിയയോട് ചേർക്കുമ്പോൾ ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങളനുസരിക്കുന്നുണ്ടെങ്കിൽ അതൊരു ഉപഗ്രൂപ്പാകുന്നു. H എന്നത് G യുടെ ഉപഗ്രൂപ്പാണെങ്കിൽ G യുടെ തൽസമകം H ൽ ഉണ്ടായിരിക്കുകയും h₁, h₂ എന്നിവ H ലെ അംഗങ്ങളാണെങ്കിൽ ഫലകം:Nowrap, h₁⁻¹ എന്നിവയും H ന്റെ അംഗങ്ങളാവുകയും ചെയ്യും.

മുകളിൽ കൊടുത്തിരിക്കുന്ന ഡൈഹെഡ്രൽ ഗ്രൂപ്പിന്റെ ഉദാഹരണത്തിൽ തൽസമകവും പരിക്രമണങ്ങളും ചേർന്ന ഉപഗണം ഫലകം:Nowrap beginR = {id, r₁, r₂, r₃}ഫലകം:Nowrap end ഒരു ഉപഗ്രൂപ്പാണ്. ഇത് കെയ്ലി പട്ടികയിൽ ചുവപ്പുനിറത്തിൽ കാണിച്ചിരിക്കുന്നു : രണ്ട് പരിക്രമണങ്ങൾ ഒന്നിനുപിറകെ ഒന്നായി ചെയ്താലുള്ള ഫലം ഒരു പരിക്രമണമായിരിക്കും, ഓരോ പരിക്രമണത്തെയും മറ്റൊരു പരിക്രമണം കൊണ്ട് തിരസ്കരിക്കാനും സാധിക്കും. H എന്ന അശൂന്യ ഉപഗണം G എന്ന ഗ്രൂപ്പിന്റെ ഉപഗ്രൂപ്പാണോ എന്ന് പരിശോധിക്കാൻ ഉപഗ്രൂപ്പ് പരിശോധന ഉപയോഗിക്കാം : ഫലകം:Nowrap beging, h ∈ Hഫലകം:Nowrap end ആവുന്ന അവസരങ്ങളിലെല്ലാം ഫലകം:Nowrap ആണെങ്കിലാണ് H ഒരു ഉപഗ്രൂപ്പാകുന്നത്. ഒരു ഗ്രൂപ്പിന്റെ ഉപഗ്രൂപ്പ് ജാലിക കണ്ടെത്തുന്നത് അതിന്റെ സവിശേഷതകൾ മനസ്സിലാക്കുന്നതിൽ വളരെയധികം സഹായിക്കുന്നു.

S എന്നത് G എന്ന ഗ്രൂപ്പിന്റെ ഉപഗണമാണെങ്കിൽ S ലെ അംഗങ്ങളുടെയും അവയുടെ വിപരിതങ്ങളുടെയും ഗുണിതങ്ങൾ മാത്രമടങ്ങിയ ഉപഗ്രൂപ്പിനെ S ജനിപ്പിക്കുന്ന ഉപഗ്രൂപ്പ് എന്നും S നെ ഉപഗ്രൂപ്പിന്റെ ജനകം എന്നും വിളിക്കുന്നു. S ലെ അംഗങ്ങളെയെല്ലാം ഉൾക്കൊള്ളുന്ന ഏറ്റവും ചെറിയ ഉപഗ്രൂപ്പാണിത്.^[29] ഡൈഹെഡ്രൽ ഗ്രൂപ്പിന്റെ ഉദാഹരണത്തിൽ r₂, f_v എന്നീ അംഗങ്ങളടങ്ങിയ ഉപഗണം ജനിപ്പിക്കുന്ന ഉപഗ്രൂപ്പ് ഈ അംഗങ്ങൾക്ക് പുറമെ തൽസമകമായ id യെയും ഫലകം:Nowrap beginf_h = f_v • r₂ഫലകം:Nowrap end എന്ന അംഗത്തെയും ഉൾക്കൊള്ളുന്നു. ഈ നാല് അംഗങ്ങൾ ചേർന്ന ഉപഗണം D₄ ന്റെ ഉപഗ്രൂപ്പാണെന്ന് കാണാൻ സാധിക്കും.

സഹഗണം

ഫലകം:Main ഗ്രൂപ്പിലെ രണ്ട് അംഗങ്ങളുടെ ഹരണഫലം ഒരു പ്രത്യേക ഉപഗ്രൂപ്പിലെ അംഗമാണെങ്കിൽ ആ അംഗങ്ങളെ സമാനമായി കണക്കാക്കാവുന്ന അവസരങ്ങളുണ്ട്. ഉദാഹരണമായി, മുകളിൽ വിശദീകരിച്ച ഡൈഹെഡ്രൽ ഗ്രൂപ്പായ D₄ ന്റെ കാര്യമെടുക്കുക. സമചതുരത്തിനുമേൽ ഒരു പ്രതിഫലനം പ്രയോഗിച്ചുകഴിഞ്ഞാൽ അതിനെ പിന്നീട് പരിക്രമണങ്ങൾ കൊണ്ട് മാത്രം r₂ എന്ന അവസ്ഥയിലേക്ക് കൊണ്ടുവരാനാകില്ല. അതായത്, സമചതുരത്തിനുമേൽ ഒരു പ്രതിഫലനം നടന്നിട്ടുണ്ടോ എന്നത് പരിക്രമണങ്ങളെ ആശ്രയിച്ചിരിക്കുന്നില്ല. ഈ ആശയത്തിന്റെ വിപുലീകരണമാണ് സഹഗണങ്ങൾ. H എന്ന ഉപഗ്രൂപ്പിനെ മുഴുവനായി g എന്ന ഏതെങ്കിലും ഗ്രൂപ്പംഗം കൊണ്ട് translate ചെയ്തതിന്റെ ഫലമായി സഹഗണങ്ങളെ മനസ്സിലാക്കാം. H എന്ന ഉപഗ്രൂപ്പിന്റെ g എന്ന അംഗമടങ്ങിയ ഇടതുസഹഗണവും വലതു സഹഗണവും യഥാക്രമം

ഫലകം:Nowrap begingH = {g • h:h ∈ H}ഫലകം:Nowrap end, ഫലകം:Nowrap beginHg = {h • g:h ∈ H}ഫലകം:Nowrap end എന്നിവയാണ്.^[30]

H എന്ന ഏതൊരു ഉപഗ്രൂപ്പിന്റെ സഹഗണങ്ങളും G യുടെ വിഭജനം തീർക്കുന്നു. അതായത്, സഹഗണങ്ങളുടെയെല്ലാം യോഗം G ആയിരിക്കും, തുല്യമല്ലാത്ത ഏത് രണ്ട് സഹഗണങ്ങളുടെയും സംഗമം ശൂന്യഗണവുമായിരിക്കും.^[31] g₁, g₂ എന്നിവ ഉൾപ്പെടുന്ന സഹഗണങ്ങളായ g₁H, g₂H എന്നിവ തുല്യമായി വരുന്നത് ഫലകം:Nowrap ആകുമ്പോൾ മാത്രമാണ്, അതായത്, സഹഗണത്തിലെ രണ്ട് അംഗങ്ങളുടെ ഹരണഫലം ഉപഗ്രൂപ്പിലെ അംഗമായിരിക്കും. സാധാരണ ഗതിയിൽ ഒരു ഉപഗ്രൂപ്പിന്റെ ഇടതും വലതും സഹഗണങ്ങൾ തുല്യമാകണമെന്നില്ല. അങ്ങനെ വരുന്ന ഉപഗ്രൂപ്പുകളെ - അതായത്, ഗ്രൂപ്പിലെ എല്ലാ അംഗങ്ങൾക്കും ഫലകം:Nowrap ആകുന്നവയെ - അഭിലംബ ഉപഗ്രൂപ്പുകൾ എന്ന് വിളിക്കുന്നു.

ഡൈഹെഡ്രൽ ഗ്രൂപ്പായ D₄ ന്റെ പരിക്രമണങ്ങൾ മാത്രമടങ്ങിയ ഉപഗ്രൂപ്പായ R ന്റെ ഇടതുസഹഗണങ്ങൾ R തന്നെയും ഫലകം:Nowrap beginU = f_cR = {f_c, f_v, f_d, f_h}ഫലകം:Nowrap end എന്ന ഗണവുമാണ്. ഈ സഹഗണത്തെ ഗ്രൂപ്പ് പട്ടികയിൽ പച്ചനിറത്തിൽ കാണിച്ചിരിക്കുന്നു. ഫലകം:Nowrap beginf_cR = U = Rf_cഫലകം:Nowrap end ആയതിനാൽ R ഒരു അഭിലംബ ഉപഗ്രൂപ്പാണ്.

ഘടകഗ്രൂപ്പുകൾ

ഫലകം:Main

ഒരു ഗ്രൂപ്പിന്റെ ഏതെങ്കിലും ഉപഗ്രൂപ്പ് അഭിലംബമാണെങ്കിൽ അതിന്റെ സഹഗണങ്ങളുടെ മേൽ ഒരു ഗ്രൂപ്പ് സംക്രിയ നിർവചിക്കാനാകും. ഇങ്ങനെ ലഭിക്കുന്ന ഗ്രൂപ്പിനെ ഘടകഗ്രൂപ്പ് അഥവാ ഹരണഫലഗ്രൂപ്പ് എന്ന് വിളിക്കുന്നു. G യുടെ അഭിലംബ ഉപഗ്രൂപ്പാണ് N എന്നുണ്ടെങ്കിൽ ഘടകഗ്രൂപ്പിനെ ഇപ്രകാരം നിർവചിക്കാം:

G / N = {gN, g ∈ G}, "G മോഡ്യുലോ N".^[32]

G ഗ്രൂപ്പിൽ നിന്ന് പകർന്നുകിട്ടുന്ന സഹഗണ ഗുണനം (അഥവാ സഹഗണ സങ്കലനം‌) ആണ് ഘടകഗ്രൂപ്പിലെ സംക്രിയ: ഫലകം:Nowrap begin(gN) • (hN) = (gh)Nഫലകം:Nowrap end. ഈ സംക്രിയ വ്യക്തമായി നിർവചിതമായിരിക്കുന്നത് ഉപഗ്രൂപ്പ് അഭിലംബമാവുമ്പോൾ മാത്രമാണ്.

ഏതൊരംഗത്തെയും അതിന്റെ സഹഗണത്തിലേക്ക് കൊണ്ടുപോകുന്ന ഫലനമായ ഫലകം:Nowrap ഒരു ഗ്രൂപ്പ് സമാംഗരൂപതയായിരിക്കാൻ വേണ്ടിയാണ് സംക്രിയ ഇപ്രകാരം നിർവചിക്കുന്നത്. ഫലകം:Nowrap begineN = Nഫലകം:Nowrap end എന്ന സഹഗണമാണ് ഘടകഗ്രൂപ്പിലെ തൽസമകം, gN എന്ന അംഗത്തിന്റെ വിപരീതം ഫലകം:Nowrap begin(gN)⁻¹ = (g⁻¹)Nഫലകം:Nowrap end എന്ന അംഗവും.

•	R	U
R	R	U
U	U	R
ഘടകഗ്രൂപ്പായ ഫലകം:Nowrap ന്റെ കെയ്ലി പട്ടിക.

ഉദാഹരണമായി, ഫലകം:Nowrap എന്ന ഘടകഗ്രൂപ്പെടുക്കുക. ഈ ഗ്രൂപ്പിലെ അംഗങ്ങൾ R തന്നെയും ഫലകം:Nowrap beginU = f_vRഫലകം:Nowrap end എന്ന സഹഗണവുമാണ്. ഈ ഗ്രൂപ്പിന്റെ കെയ്ലി പട്ടിക വലതുഭാഗത്ത് കൊടുത്തിരിക്കുന്നു. ഫലകം:Nowrap beginR = {id, r₁, r₂, r₃}ഫലകം:Nowrap end എന്ന ഉപഗ്രൂപ്പും അതിന്റെ ഘടകഗ്രൂപ്പും ക്രമഗ്രൂപ്പുകളാണ്, എന്നാൽ മാതൃഗ്രൂപ്പായ D₄ ക്രമഗ്രൂപ്പല്ല. R, ഫലകം:Nowrap എന്നീ ഗ്രൂപ്പുകളിൽ നിന്ന് D₄ നെ നിർമ്മിക്കുന്നതുപോലെ ചെറിയ ഗ്രൂപ്പുകളിൽ നിന്ന് വലിയ ഗ്രൂപ്പുകളെ നിർമ്മിക്കാൻ സഹായിക്കുന്ന അമൂർത്ത ആശയമാണ് അർദ്ധനേർ ഉല്പന്നം.

ഉപഗ്രൂപ്പുകളെയും ഘടകഗ്രൂപ്പുകളെയുമുപയോഗിച്ച് ഏതൊരു ഗ്രൂപ്പിനെയും അതിന്റെ പ്രെസന്റേഷൻ വഴി വർണ്ണിക്കാവുന്നതാണ്. ഏതൊരു ഗ്രൂപ്പും അതിന്റെ ജനകങ്ങളുടെ സ്വതന്ത്രഗ്രൂപ്പിനെ അതിന്റെ ബന്ധങ്ങളുടെ ഉപഗ്രൂപ്പുകൊണ്ട് ഹരിച്ചുകിട്ടുന്ന ഘടകഗ്രൂപ്പാണ്. D₄ എന്ന ഡൈഹെഡ്രൽ ഗ്രൂപ്പിന്റെ ജനകങ്ങൾ r എന്ന ഒരു 90° പരിക്രമണവും f എന്ന ഒരു പ്രതിഫലനവുമാണ് (ഉദാഹരണമായി, r = r₁, f = f_v എന്നെടുക്കാം) - അതായത്, ഗ്രൂപ്പിലെ മറ്റേതംഗത്തെയും ഈ അംഗങ്ങളുടെയും അവയുടെ വിപരീതങ്ങളുടെയും മേൽ ഗ്രൂപ്പ് സംക്രിയ പ്രയോഗിച്ച് നിർമ്മിക്കാവുന്നതാണ്. ഈ അംഗങ്ങളോടൊപ്പം

r ⁴ = f ² = (r • f)² = 1,^[33]

എന്ന ബന്ധങ്ങളും കൂടി ഉപയോഗിച്ചാൽ ഗ്രൂപ്പിനെ പൂർണ്ണമായി വർണ്ണിക്കാം. ഗ്രൂപ്പിന്റെ കെയ്ലി ഗ്രാഫ് നിർമ്മിക്കാനും അതിന്റെ പ്രെസന്റേഷൻ ഉപയോഗിച്ച് സാധിക്കും.

ഉദാഹരണങ്ങളും പ്രയോഗങ്ങളും

ഫലകം:Multiple image

ഗ്രൂപ്പുകൾക്ക് ഗണിതത്തിനകത്തും പുറത്തും വളരെയേറെ ഉദാഹരണങ്ങളും പ്രയോഗങ്ങളുമുണ്ട്. മുകളിൽ വിവരിച്ച പൂർണ്ണസംഖ്യകളുടെ സങ്കലനഗ്രൂപ്പ് ഗ്രൂപ്പുകളെ മനസ്സിലാക്കുന്നതിൽ ആദ്യപടിയാണ്. സങ്കലനത്തിനു പകരം ഗുണനം സംക്രിയയായുള്ള ഗ്രൂപ്പുകളാണ് ഗുണനഗ്രൂപ്പുകൾ. അമൂർത്തബീജഗണിതത്തിൽ പ്രാധാന്യമുള്ള ഘടനകളുടെ അടിസ്ഥാനമാണിവ.

ഗ്രൂപ്പുകൾക്ക് മറ്റ് ഗണിതശാഖകളിലും പ്രയോഗങ്ങളുണ്ട്. ഗണിതവ്യൂഹങ്ങളെ ഗ്രൂപ്പുകളുമായി ബന്ധപ്പെടുത്തി ആ ഗ്രൂപ്പുകളുടെ സവിശേഷതകൾ പഠിക്കുന്നത് ഗണിതവ്യൂഹങ്ങളെ കൂടുതൽ മനസ്സിലാക്കാൻ സഹായിക്കുന്നു. ഉദാഹരണമായി, ഹെൻറി പോങ്കാരെ ബീജീയ സംസ്ഥിതി എന്ന ശാഖക്ക് തുടക്കം കുറിച്ചത് അടിസ്ഥാനഗ്രൂപ്പ് എന്ന ആശയം മുന്നോട്ടുവച്ചുകൊണ്ടാണ്.^[34] ഈ ആശയമുപയോഗിച്ച് സംസ്ഥിതിയിലെ സാമീപ്യം, സന്തതി മുതലായ ആശയങ്ങളെ ഗ്രൂപ്പ് ആശയങ്ങളുമായി ബന്ധപ്പെടുത്താനാകുന്നു. ഉദാഹരണമായി, അടിസ്ഥാനഗ്രൂപ്പിലെ അംഗങ്ങൾ വളയങ്ങളാണ്. വലതുഭാഗത്തെ രണ്ടാമത്തെ ചിത്രം ഒരു പ്രതലത്തിൽ നിന്ന് ഒരു ബിന്ദു നീക്കിയാൽ കിട്ടുന്ന ജ്യാമിതിയുടെ അടിസ്ഥാനഗ്രൂപ്പിലെ അംഗങ്ങളായ വളയങ്ങളെ കാണിക്കുന്നു. നീല വളയത്തെ സന്തതമായി ചുരുക്കിക്കൊണ്ട് ഒരു ബിന്ദുവായി മാറ്റാമെന്നതിനാൽ അത് null-homotopic ആണ്, അതിനാൽ അപ്രധാനവും. എന്നാൽ ഓറഞ്ച് നിറത്തിലെ വളയത്ത് ഇങ്ങനെ ചുരുക്കുന്നതിൽ നിന്ന് കേന്ദ്രത്തിലെ ബിന്ദു തടയുന്നു. ബിന്ദു ഒഴിവാക്കിയ പ്രതലത്തിന്റെ അടിസ്ഥാനഗ്രൂപ്പ് അനന്തവും ചാക്രികവുമാണ്. ഓറഞ്ച് വളയം (അഥവാ നീക്കപ്പെട്ട ബിന്ദുവിന് ചുറ്റും ഒരു തവണ കറങ്ങുന്ന ഏതെങ്കിലും വളയം) ഈ ഗ്രൂപ്പിന്റെ ജനകമാണ്. അതായത്, അടിസ്ഥാനഗ്രൂപ്പിന് പ്രതലത്തിലെ തുള കണ്ടുപിടിക്കാൻ സാധിക്കുന്നു.

ബഹിർവലയഗ്രൂപ്പുകൾ ഉൾപ്പെടെയുള്ള ഗ്രൂപ്പുകളെ പഠിക്കാൻ ജ്യാമിതീയ ഗ്രൂപ്പ് സിദ്ധാന്തം എന്ന ശാഖ ജ്യാമിതീയ ആശയങ്ങളെ ഉപയോഗിക്കുന്നു.^[35] ബീജീയജ്യാമിതി, സംഖ്യാസിദ്ധാന്തം എന്നിവ ഗ്രൂപ്പ് ആശയങ്ങൾ വ്യാപകമായി ഉപയോഗിക്കപ്പെടുന്ന ശാഖകളാണ്.^[36]

മേല്പറഞ്ഞ ശാഖകളിലേതുപോലെ ഗ്രൂപ്പുകൾക്ക് സൈദ്ധാന്തികപ്രാധാന്യം മാത്രമല്ല ഉള്ളത്. അമൂർത്ത ഗ്രൂപ്പ് ആശയങ്ങളെയും കമ്പ്യൂട്ടേഷണൽ ഗ്രൂപ്പ് സിദ്ധാന്തത്തിലെ അൽഗൊരിതങ്ങളെയും പ്രായോഗികതലത്തിൽ ഉപയോഗിക്കുന്ന ശാഖയാണ് ഗൂഢശാസ്ത്രം. പരിബദ്ധഗ്രൂപ്പുകളാണ് ഗൂഢശാസ്ത്രത്തിൽ കൂടുതലായി കൈകാര്യം ചെയ്യപ്പെടുന്നത്.^[37]

ഗണിതത്തിനു പുറമെ ഭൗതികശാസ്ത്രം, രസതന്ത്രം, കമ്പ്യൂട്ടർ സയൻസ് എന്നീ ശാസ്ത്രശാഖകളിലും വിവിധ ആവശ്യങ്ങൾക്ക് ഗ്രൂപ്പ് ആശയങ്ങൾ ഉപയോഗിക്കപ്പെടുന്നു.

സംഖ്യകൾ

പൂർണ്ണസംഖ്യകൾ, ഭിന്നകസംഖ്യകൾ മുതലായ സംഖ്യാവ്യവസ്ഥകൾക്ക് ഗ്രൂപ്പ് ഘടനയുണ്ട്. ഭിന്നകസംഖ്യകളുൾപ്പെടെയുള്ള ചില വ്യവസ്ഥകൾ സങ്കലനത്തിനു കീഴിലും ഗുണനത്തിനു കീഴിലും ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങളനുസരിക്കുന്നു, അവയ്ക്ക് ഗ്രൂപ്പ് ഘടനയ്ക്കു പുറമെ വലയ, ക്ഷേത്ര ഘടനകകളുമുണ്ടാകും. അമൂർത്ത ബീജഗണിതത്തിലെ മറ്റ് ആശയങ്ങളായ മോഡ്യൂളുകൾ, സദിശസമഷ്ടികൾ, ആൾജിബ്രകൾ എന്നിവയ്ക്കും ഗ്രൂപ്പ് ഘടനയുണ്ട്.

പൂർണ്ണസംഖ്യകൾ

പൂർണ്ണസംഖ്യാഗണമായ Z സങ്കലനത്തിനുകീഴിൽ മുകളിൽ വിശദീകരിച്ചതുപോലെ (Z, +) എന്ന ഗ്രൂപ്പ് സൃഷ്ടിക്കുന്നു. എന്നാൽ സങ്കലനത്തിനുപകരം ഗുണനം സംക്രിയയാക്കിയാൽ (Z, ·) ഗ്രൂപ്പാവുകയില്ല. സംവൃതിനിയമം, സാഹചര്യനിയമം, തൽസമകത്തിന്റെ അസ്തിത്വം എന്ന ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങൾ അനുസരിക്കപ്പെടുന്നുണ്ടെങ്കിലും ഗണത്തിലെ എല്ലാ അംഗങ്ങൾക്കും വിപരിത അംഗങ്ങളില്ല എന്നതാണ് കാരണം. ഉദാഹരണമായി, ഫലകം:Nowrap begina = 2ഫലകം:Nowrap end ഒരു പൂർണ്ണസംഖ്യയാണെങ്കിലും ഫലകം:Nowrap begina · b = 1ഫലകം:Nowrap end എന്ന സമവാക്യത്തിന്റെ ഒരേയൊരു നിർദ്ധാരണമായ b = 1/2 ഒരു പൂർണ്ണസംഖ്യയല്ല.

ഭിന്നകങ്ങൾ

ഗുണനത്തിലും സംഖ്യകൾക്ക് വിപരീതം വേണം എന്നതിനാൽ ഭിന്നസംഖ്യകൾ ഉപയോഗിച്ചുനോക്കാം:

\frac{a}{b}

b പൂജ്യമല്ലാത്ത പൂർണ്ണസംഖ്യകളുടെ ഹരണഫലങ്ങളെ ഭിന്നകസംഖ്യകൾ എന്ന് വിളിക്കുന്നു. ഭിന്നകസംഖ്യകളുടെ ഗണത്തെ Q എന്നാണ് സൂചിപ്പിക്കുന്നത്. ഗുണനം സംക്രിയയായുള്ള ഭിന്നസംഖ്യാഗണം ഫലകം:Nowrap ഇപ്പോഴും ഒരു ഗ്രൂപ്പായിട്ടില്ല. കാരണം, ഭിന്നസംഖ്യയായ പൂജ്യത്തിന് ഗുണനവിപരിതമില്ല. അതായത്, ഫലകം:Nowrap beginx · 0 = 1ഫലകം:Nowrap end എന്ന സമവാക്യമനുസരിക്കുന്ന x എന്ന ഭിന്നകമില്ലാത്തതിനാൽ (Q, ·) ഒരു ഗ്രൂപ്പല്ല.

എന്നാൽ പൂജ്യമൊഴികെയുള്ള ഭിന്നകസംഖ്യകളുടെ ഗണമായ ഫലകം:Nowrap beginQ \ {0} = {q ∈ Q, q ≠ 0}ഫലകം:Nowrap end ഗുണനത്തിനു കീഴിൽ ഒരു ക്രമഗ്രൂപ്പ് സൃഷ്ടിക്കുന്നു ഫലകം:Nowrap അഥവാ ഫലകം:Nowrap എന്നാണ് ഈ ഗ്രൂപ്പിനെ സൂചിപ്പിക്കുന്നത്. സാഹചര്യനിയമവും തൽസമക അസ്തിത്വനിയമവും ഗുണനത്തിന്റെ പ്രത്യേകതകൾ മൂലം അനുസരിക്കപ്പെടുന്നു. പൂജ്യമല്ലാത്ത രണ്ട് ഭിന്നകസംഖ്യകളുടെ ഗുണനഫലം ഒരിക്കലും പൂജ്യമാകാത്തതിനാൽ സംവൃതിനിയമവും, a/b യുടെ ഗുണനവിപരിതം b/a ആയതിനാൽ വിപരീത അസ്തിത്വനിയമവും ഗ്രൂപ്പ് അനുസരിക്കുന്നു.

പൂജ്യമുൾപ്പെടെയുള്ള ഭിന്നകങ്ങളുടെ ഗണം സങ്കലനത്തിനുകീഴിലും ഒരു ഗ്രൂപ്പാണ്. ഒരേ ഗണത്തിൽ തന്നെ ഈവിധം സങ്കലനവും ഗുണനവും ചെയ്യുന്നത് കൂടുതൽ സങ്കീർണ്ണമായ ബീജീയഘടനയായ വലയങ്ങൾ നിർമ്മിക്കുന്നു. Q ഗണത്തിലെപ്പോലെ വലയത്തിൽ ഹരണവും സാധ്യമാണെങ്കിൽ ബീജീയഘടനയെ ക്ഷേത്രം എന്ന് വിളിക്കുന്നു, ക്ഷേത്രങ്ങൾക്ക് അമൂർത്തബീജഗണിതത്തിലും കമ്പ്യൂട്ടർ സയൻസിലും സുപ്രധാന സ്ഥാനമാണുള്ളത്. ഈ ബീജീയഘടനകളുടെ സവിശേഷതകൾ വിവരിക്കുന്നതിലും ഗ്രൂപ്പ് സിദ്ധാന്തത്തിലെ നിയമങ്ങൾ സഹായിക്കുന്നു.

പൂർണ്ണസംഖ്യകളുടെ മോഡ്യുലോ അഭാജ്യസംഖ്യയായുള്ള ഗ്രൂപ്പ്

p ഒരു അഭാജ്യസംഖ്യയാണെങ്കിൽ പൂർണ്ണസംഖ്യകളെ p കൊണ്ട് ഹരിച്ചാൽ കിട്ടുന്ന അശൂന്യ ശിഷ്ടങ്ങൾ ഒരു ഗ്രൂപ്പ് സൃഷ്ടിക്കുന്നു.^[38] p കൊണ്ട് ഹരിക്കാനാവാത്ത പൂർണ്ണസംഖ്യകളാണ് ഈ ഗ്രൂപ്പിലെ അംഗങ്ങൾ, എന്നാൽ ഈ സംഖ്യകളെ മോഡ്യുലോ p ആയാണ് കണക്കിലെടുക്കുക. അതായത്, രണ്ട് സംഖ്യകളുടെ വ്യത്യാസം p യുടെ ഗുണിതമാണെങ്കിൽ അവയെ തുല്യമായി കണക്കാക്കുന്നു. ഇങ്ങനെ നോക്കുമ്പോൾ 1 മുതൽ p-1 വരെയുള്ള സംഖ്യകളാണ് ഗ്രൂപ്പിലെ അംഗങ്ങൾ എന്നും പറയാം. ഉദാഹരണമായി, ഫലകം:Nowrap beginp = 5ഫലകം:Nowrap end ആണെങ്കിൽ ഗ്രൂപ്പിലെ അംഗങ്ങൾ 1, 2, 3, 4 എന്നിവയാണ്: അഞ്ചിന്റെ ഗുണിതങ്ങൾ ഗ്രൂപ്പിലെ അംഗങ്ങളല്ല; 6, -4 മുതലായ സംഖ്യകൾ 1 ന് തുല്യമായാണ് കണക്കാക്കുക താനും. ഗുണനമാണ് ഗ്രൂപ്പ് സംക്രിയ. ഈ ഗ്രൂപ്പിൽ ഫലകം:Nowrap begin4 · 4 = 1ഫലകം:Nowrap end ആണ്. സാധാരണ രീതിയിലുള്ള ഗുണിതമായ 16 ഈ ഗ്രൂപ്പിൽ 1 ന് തുല്യമാണ് (ഫലകം:Nowrap begin16 − 1 = 15ഫലകം:Nowrap end, ഇത് അഞ്ചിന്റെ ഗുണിതമാണ്) എന്നതാണിതിന് കാരണം. ഇതിനെ 16 ≡ 1 (mod 5) എന്നിങ്ങനെ സൂചിപ്പിക്കുന്നു.

p ഒരു അഭാജ്യസംഖ്യയായതിനാൽ p യുടെ ഗുണിതമല്ലാത്ത രണ്ട് സംഖ്യഗളുടെ ഗുണനഫലവും p യുടെ ഗുണിതമായിരിക്കുകയില്ല. അതിനാൽ ഈ ഗ്രൂപ്പ് സംവൃതിനിയമമനുസരിക്കുന്നുവെന്ന് കാണാം. ഗ്രൂപ്പിലെ തൽസമകം സാധാരണ ഗുണനത്തിലേതുപോലെ 1 ആണ്. പൂർണ്ണസംഖ്യകളുടെ ഗുണനത്തിന്റെ സാഹചര്യനിയമം ഗ്രൂപ്പ് സംക്രിയയിലേക്കും പകർന്നുകിട്ടുന്നു. നാലാമത്തെ ഗ്രൂപ്പ് സ്വയംപ്രമാണം പാലിക്കപ്പെടണമെങ്കിൽ p യുടെ ഗുണിതമല്ലാത്ത ഏതൊരു a യ്ക്കും

a · b ≡ 1 (mod p), അതായത് p യുടെ ഗുണിതമാണ് ഫലകം:Nowrap

എന്ന തരത്തിൽ ഒരു b ഉണ്ടായിരിക്കണം. [[ഉത്തമ സാധാരണ ഘടകം|ഫലകം:Nowrap]] ആയതിനാൽ അത്തരമൊരു b ഉണ്ടെന്ന് വരുന്നു, ബെസൗ അനന്യത ഉപയോഗിച്ച് ഇത് കണ്ടുപിടിക്കുകയും ചെയ്യാം.^[39] ഫലകം:Nowrap beginp = 5ഫലകം:Nowrap end ആണെങ്കിൽ 4 ന്റെ വിപരിതം 4 ഉം, 3 ന്റെ വിപരിതം 2 ഉമാണ് (ഫലകം:Nowrap begin3 · 2 = 6 ≡ 1 (mod 5)ഫലകം:Nowrap end). അതായത്, ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങളെല്ലാം ഇവിടെ പാലിക്കപ്പെടുന്നു.

മോഡ്യുലോ അഭാജ്യസംഖ്യയായുള്ള (p) പൂർണ്ണസംഖ്യകളുടെ ഗ്രൂപ്പ് യഥാർത്ഥത്തിൽ പരിബദ്ധക്ഷേത്രമായ F_p യുടെ ഗുണനഗ്രൂപ്പാണ്. F_p^× എന്നാണ് ഈ ഗ്രൂപ്പിനെ സൂചിപ്പിക്കുക. മുകളിൽ വിവരിച്ച ഗ്രൂപ്പായ (Q\{0}, ·) ന് സമാനമാണ് ഈ ഗ്രൂപ്പ്.^[40] ഈ ഗ്രൂപ്പുകൾ പബ്ലിക് കീ ഗൂഢശാസ്ത്രത്തിൽ പ്രധാന പങ്കു വഹിക്കുന്നു.

ചാക്രികഗ്രൂപ്പുകൾ

ഫലകം:Main

ഒരു ഗ്രൂപ്പിലെ എല്ലാ അംഗങ്ങളും ഒരു പ്രത്യേക അംഗത്തിന്റെ ഘാതങ്ങളായി (ഗുണനരിതിയിൽ എഴുതുമ്പോഴാണിത്, സങ്കലനരീതിയിലെഴുതുമ്പോൾ ഗുണിതങ്ങൾ) വരുന്നുവെങ്കിൽ ആ ഗ്രൂപ്പിനെ ചാക്രികഗ്രൂപ്പ് എന്ന് വിളിക്കുന്നു.^[41] ഒരു ചാക്രികഗ്രൂപ്പിലെ അംഗങ്ങൾ

..., a⁻³, a⁻², a⁻¹, a⁰ = e, a, a², a³, ...,

എന്നിവയായിരിക്കും. ഇവിടെ ഫലകം:Nowrap, ഫലകം:Nowrap എന്നിങ്ങനെയാണ് ഉദ്ദേശിക്കുന്നത്. a എന്ന അംഗത്തെ ഗ്രൂപ്പിന്റെ ജനകം അഥവാ primitive element എന്ന് വിളിക്കുന്നു.

ഒന്നിന്റെ n-ആം മിശ്രസംഖ്യാമൂലങ്ങളുടെ ഗ്രൂപ്പ് ചാക്രികഗ്രൂപ്പിന് ഉദാഹരണമാണ്. ഈ ഗ്രൂപ്പിലെ അംഗങ്ങൾ ഫലകം:Nowrap beginzⁿ = 1ഫലകം:Nowrap end എന്ന സമവാക്യമനുസരിക്കുന്ന മിശ്രസംഖ്യകളും സംക്രിയ ഗുണനവുമാണ്.^[42] n അംഗങ്ങളുള്ള ഏത് ചാക്രികഗ്രൂപ്പും ഈ ഗ്രൂപ്പിന് സമരൂപമാണ്. ക്ഷേത്രസിദ്ധാന്തമുപയോഗിച്ച് F_p^× എന്ന ഗ്രൂപ്പ് ചാക്രികമാണെന്ന് തെളിയിക്കാനാകും. ഉദാഹരണമായി, ഫലകം:Nowrap beginp = 5ഫലകം:Nowrap end ആണെങ്കിൽ 3 ഈ ഗ്രൂപ്പിന്റെ ജനകമാണ് (ഫലകം:Nowrap begin3¹ = 3,ഫലകം:Nowrap end ഫലകം:Nowrap begin3² = 9 ≡ 4,ഫലകം:Nowrap end ഫലകം:Nowrap begin3³ ≡ 2,ഫലകം:Nowrap end ഫലകം:Nowrap begin3⁴ ≡ 1.ഫലകം:Nowrap end).

ചില ചാക്രികഗ്രൂപ്പുകളിലെ അംഗങ്ങളുടെ എണ്ണം അനന്തമാണ്. ഈ ഗ്രൂപ്പുകളിൽ തൽസമകമല്ലാത്ത ഏതൊരംഗം a ക്കും, a യുടെ ഘാതങ്ങളെല്ലാം വ്യത്യസ്തമാണ്. അതായത്, ചാക്രികഗ്രൂപ്പ് എന്ന പേരുണ്ടെങ്കിലും, ഈ ഗ്രൂപ്പിലെ അംഗങ്ങളെ വീണ്ടും വീണ്ടും ഗുണിച്ച് തുടങ്ങിയേടത്തു തന്നെ എത്തിച്ചേരാനാകില്ല. അനന്തചാക്രികഗ്രൂപ്പുകളെല്ലാം പൂർണ്ണസംഖ്യകളുടെ സങ്കലനഗ്രൂപ്പായ (Z, +) ന് സമരൂപമാണ്.^[43]

ക്രമഗ്രൂപ്പുകൾ

ഫലകം:Main ഒരു ഗ്രൂപ്പിന്റെ സംക്രിയ ഗ്രൂപ്പിലെ അംഗങ്ങളുടെ മേൽ ക്രമനിയമം പാലിക്കുന്നുവെങ്കിൽ ആ ഗ്രൂപ്പിനെ ക്രമഗ്രൂപ്പ് അഥവാ ആബേലിയൻ ഗ്രൂപ്പ് എന്ന് വിളിക്കുന്നു. അതായത്, ഗ്രൂപ്പിലെ ഏത് രണ്ട് അംഗങ്ങളുടെമേൽ സംക്രിയ ഉപയോഗിച്ചാലും കിട്ടുന്ന ഉത്തരം അംഗങ്ങളുടെ ക്രമത്തെ ആശ്രയിക്കരുത്. (G,•) എന്ന ക്രമഗ്രൂപ്പിലെ അംഗങ്ങളാണ് a, b എങ്കിൽ a • b = b • a എന്ന് വരും.

മുകളിൽ ചാക്രികഗ്രൂപ്പുകളെക്കുറിച്ചുള്ള ഭാഗത്ത് വിശദീകരിച്ച രണ്ടുതരം ഗ്രൂപ്പുകളും ക്രമഗ്രൂപ്പുകളായതിനാൽ ചാക്രികഗ്രൂപ്പുകളെല്ലാം ക്രമഗ്രൂപ്പുകളാണെന്ന് കാണാം. ക്രമഗ്രൂപ്പുകളെക്കുറിച്ചുള്ള പഠനം വളരെയധികം വികസിച്ച ഒരു ഗ്രൂപ്പ് സിദ്ധാന്തശാഖയാണ്. പരിബദ്ധ ക്രമഗ്രൂപ്പുകളുടെ വർഗ്ഗീകരണം ഈ വിഷയത്തിലെ ഒരു പ്രധാന ഗവേഷണഫലമാണ്. ഗ്രൂപ്പ് കേന്ദ്രം, ക്രമവിനിമയകം മുതലായ ആശയങ്ങൾ ഒരു ഗ്രൂപ്പ് ക്രമഗ്രൂപ്പിൽ നിന്ന് എത്രത്തോളം വ്യതിചലിക്കുന്നു എന്ന് മനസ്സിലാക്കാൻ സഹായിക്കുന്നു.^[44]

സമമിതിഗ്രൂപ്പുകൾ

ഗണിതവ്യൂഹങ്ങളുടെ സമമിതികൾ വിശദീകരിക്കുന്ന ഗ്രൂപ്പുകളാണ് സമമിതിഗ്രൂപ്പുകൾ. സമമിതികൾ മുകളിൽ വിശദീകരിച്ച ഡൈഹെഡ്രൽ ഗ്രൂപ്പിലേതുപോലെ ജ്യാമിതീയമോ ബഹുപദസമവാക്യങ്ങളുടെ നിർദ്ധാരണങ്ങളുടേതുപോലെ ബീജീയമോ ആകാം.^[45] ഗ്രൂപ്പ് സിദ്ധാന്തത്തെ സമമിതികളുടെ പഠനമായി കാണാവുന്നതാണ്. സമമിതികൾ മനസ്സിലാക്കുന്നത് ഗണിതവ്യൂഹങ്ങളുടെ പഠനത്തിൽ വളരെയേറെ സഹായിക്കുന്നു. ഒരു ഗ്രൂപ്പിലെ എല്ലാ അംഗങ്ങളും ഏതെങ്കിലും ഗണിതവസ്തുവിനുമേൽ ഗ്രൂപ്പ് നിയമത്തിനനുസൃതമായ ഏതെങ്കിലും ക്രിയ ചെയ്യുന്നുവെങ്കിൽ ആ ഗ്രൂപ്പ് ഗണിതവസ്തുവിനുമേൽ പ്രവർത്തിക്കുന്നതായി കണക്കാക്കുന്നു. ഉദാഹരണമായി, താഴെ വലതുഭാഗത്തായി കൊടുത്തിരിക്കുന്ന ഘടനയുടെമേൽ (2,3,7) ത്രികോണഗ്രൂപ്പ് ചെയ്യുന്ന ക്രിയ പച്ചനിറത്തിലുള്ള ത്രികോണങ്ങളെ (മറ്റുള്ളവയെയും) ക്രമചയത്തിന് വിധേയമാക്കുകയാണ്. ഗ്രൂപ്പ് പ്രവർത്തനം വഴി ഗ്രൂപ്പിന്റെ ഘടന അത് പ്രവർത്തിക്കുന്ന ഗണിതവസ്തുവിന്റെ ഘടനയുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു.

ക്രിസ്റ്റലോഗ്രഫി മുതലായ രസതന്ത്രശാഖകളിൽ സ്പേസ് ഗ്രൂപ്പുകളും പോയിന്റ് ഗ്രൂപ്പുകളും തന്മാത്രകളുടെയും പരലുകളുടെയും സമമിതികൾ വിശദീകരിക്കുന്നു. ഇവയുടെ രാസ, ഭൗതിക സവിശേഷതകൾ നിശ്ചയിക്കുന്നതിൽ സമമിതികൾക്ക് പ്രധാന പങ്കുണ്ട്. ഈ സവിശേഷതകളെക്കുറിച്ചുള്ള ക്വാണ്ടം ഭൗതിക പഠനം എളുപ്പമാക്കാൻ ഗ്രൂപ്പ് സിദ്ധാന്തം സഹായിക്കുന്നു.^[46] ഉദാഹരണമായി, ചില ക്വാണ്ടം നിലകൾക്കിടയിൽ പ്രകാശിക അവസ്ഥാന്തരണം സാധ്യമല്ലെന്ന് നിലകളുടെ സമമിതികളിൽ നിന്ന് മനസ്സിലാക്കാം. ചില അവസരങ്ങളിൽ തന്മാത്രകൾക്ക് സമമിതിയിൽ വ്യത്യാസം വരുന്നത് പ്രവചിക്കാനും ഗ്രൂപ്പ് സിദ്ധാന്തത്തിന് സാധിക്കുന്നു. ഉയർന്ന സമമിതിയുള്ള ചില തന്മാത്രകൾ അസ്ഥിരമായിരിക്കുമെന്നും അതിനാൽ സമമിതി കുറയ്ക്കാൻ വേണ്ടി അവ ജ്യാമിതീയഘടനയിൽ വ്യത്യാസം വരുത്തുമെന്നും ഹെർമൻ ആർതർ യാൻ, എഡ്വേഡ് ടെല്ലർ എന്നിവർ ഗ്രൂപ്പ് സിദ്ധാന്തമുപയോഗിച്ച് തെളിയിച്ചു. ഈ പ്രതിഭാസത്തെ യാൻ-ടെല്ലർ പ്രഭാവം എന്ന് വിളിക്കുന്നു.^[47]^[48]

അവസ്ഥാന്തരണത്തിന് വിധേയമാകുന്ന വസ്തുക്കളുടെ ഭൗതികസവിശേഷതകളിലെ വ്യത്യാസം പ്രവചിക്കാനും ഗ്രൂപ്പ് സിദ്ധാന്തത്തിന്റെ സഹായം തേടാം. ഉദാഹരണമായി, ക്യൂബിക് പരലാകൃതിയിൽ നിന്ന് ടെട്രാഹെഡ്രൽ പരലാകൃതിയിലേക്ക് ഒരു വസ്തൂ മാറുമ്പോൾ അതിന്റെ സമമിതിയിൽ വ്യത്യാസം വരുന്നു. പാരാഇലക്ട്രിക് അവസ്ഥയിൽ നിന്ന് ഫെറോഇലക്ട്രിക് അവസ്ഥയിലേക്ക് ക്യൂറി താപനിലയിൽ വച്ച് പദാർത്ഥങ്ങൾക്ക് അവസ്ഥാന്തരണമുണ്ടാവുമ്പോൾ അവ ഉയർന്ന സമമിതിയുള്ള അവസ്ഥയിൽ നിന്ന് താഴ്ന്ന സമമിതിയുള്ള അവസ്ഥയിലേക്കാണ് മാറുന്നത്.^[49]

കണികാഭൗതികത്തിലും സമമിതിനഷ്ടം പ്രാധാന്യമർഹിക്കുന്നുണ്ട്. ഇത് ഗോൾഡ്സ്റ്റോൺ ബോസോണുകളുടെ ആവിർഭാവവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു


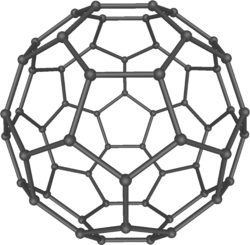
ബക്മിൻസ്റ്റർഫുള്ളെറിൻ ഐകോസാഹെഡ്രൽ സമമിതി കാണിക്കുന്നു	അമോണിയയുടെ (NH₃) സമമിതിഗ്രൂപ്പ് D₃ ആണ്. പ്രതിഫലനവും 120° പരിക്രമണവുമാണ് ജനകങ്ങൾ	ക്യൂബേൻ (C₈H₈) ഒക്ടാഹെഡ്രൽ സമമിതി കാണിക്കുന്നു	[Cu(OH₂)₆]²⁺ അയോൺ. യാൻ-ടെല്ലർ പ്രഭാവം മൂലം പൂർണ്ണ സമമിതീയരൂപത്തിൽ നിന്ന് ലംബദിശയിൽ 22% വ്യതിയാനം കാണിക്കുന്നു	ബഹിർവലയഗ്രൂപ്പായ (2,3,7) ത്രികോണഗ്രൂപ്പ് ബഹിർവലയപ്രതലത്തിന്റെ ഈ ടൈലിങ്ങിനുമേൽ പ്രവർത്തിക്കുന്നു

മാത്യൂ ഗ്രൂപ്പുകൾ ഉൾപ്പെടെയുള്ള പരിബദ്ധ സമമിതിഗ്രൂപ്പുകൾ കോഡിങ്ങ് സിദ്ധാന്തത്തിലും ഉപയോഗിക്കപ്പെടുന്നു. സിഡി പ്ലെയറുകളിലും അയക്കുന്ന വിവരങ്ങളിലെ തെറ്റുകൾ തിരുത്തുന്നതിലും ഇത് ഉപയോഗം കാണുന്നു.^[50] ഡിഫറെൻഷ്യൽ ഗാൽവ സിദ്ധാന്തം, ജ്യാമിതീയ നിശ്ചരസിദ്ധാന്തം എന്നിവയും സമമിതിഗ്രൂപ്പുകളുടെ പ്രയോഗമേഖലകളാണ്.^[51]

സാമാന്യ രേഖീയഗ്രൂപ്പും പ്രാതിനിധ്യസിദ്ധാന്തവും

മാട്രിക്സുകൾ അംഗങ്ങളും മാട്രിക്സ് ഗുണനം സംക്രിയയുമായുള്ള ഗ്രൂപ്പുകളാണ് മാട്രിക്സ് ഗ്രൂപ്പുകൾ. സാരണികം പൂജ്യമല്ലാത്തതും (അതായത്, ഗുണനവിപരീതമുള്ളവ) അംഗങ്ങൾ വാസ്തവികസംഖ്യകളുമായ n×n മാട്രിക്സുകളുടെ ഗ്രൂപ്പാണ് ഫലകം:Nowrap beginGL(n, R)ഫലകം:Nowrap end എന്ന് സൂചിപ്പിക്കുന്ന സാമാന്യ രേഖീയഗ്രൂപ്പ്.^[52] ഇവയുടെ ഉപഗ്രൂപ്പുകളെയാണ് മാട്രിക്സ് ഗ്രൂപ്പുകൾ അഥവാ രേഖീയഗ്രൂപ്പുകൾ എന്ന് വിളിക്കുന്നത്. മുകളിൽ വിവരിച്ച ഡൈഹെഡ്രൽ ഗ്രൂപ്പ് ഒരു ചെറിയ മാട്രിക്സ് ഗ്രൂപ്പാണ്. n മാനങ്ങളിലെ എല്ലാ പരിക്രമണങ്ങളെയും സൂചിപ്പിക്കുന്ന മാട്രിക്സുകളടങ്ങിയ വിശിഷ്ട ഓർത്തോഗണൽ ഗ്രൂപ്പ് SO(n) ഒരു പ്രധാന മാട്രിക്സ് ഗ്രൂപ്പാണ്. ഓയ്ലർ കോണുകൾ വഴി പരിക്രമണമാട്രിക്സുകൾ കമ്പ്യൂട്ടർ ഗ്രാഫിക്സിൽ ഉപയോഗിക്കപ്പെടുന്നു.^[53]

ഗ്രൂപ്പുകളെ കൂടുതൽ ആഴത്തിൽ മനസ്സിലാക്കാൻ സഹായിക്കുന്ന ഒരു ശാഖയാണ് പ്രാതിനിധ്യസിദ്ധാന്തം.^[54]^[55] മറ്റ് സമഷ്ടികളുടെമേലുള്ള ഗ്രൂപ്പ് പ്രവർത്തനം വഴിയാണ് പ്രാതിനിധ്യസിദ്ധാന്തം ഗ്രൂപ്പുകളെ പഠിക്കുന്നത്. ഗ്രൂപ്പ് പ്രവർത്തനങ്ങൾ ത്രിമാന യൂക്ലിഡിയൻ സമഷ്ടി (R³) ഉൾപ്പെടെയുള്ള സദിശസമഷ്ടികളുടെ മേലാണെങ്കിൽ ആ ഗ്രൂപ്പ് പ്രാതിനിധ്യങ്ങളെ രേഖീയ പ്രാതിനിധ്യങ്ങൾ എന്ന് വിളിക്കുന്നു. G എന്ന ഗ്രൂപ്പിന്റെ n മാനങ്ങളുള്ള വാസ്തവിക സദിശസമഷ്ടിക്കുമേലുള്ള പ്രാതിനിധ്യം ഗ്രൂപ്പിൽ നിന്ന് സാമാന്യ രേഖീയഗ്രൂപ്പിലേക്കുള്ള

ρ: G → GL(n, R)

എന്ന ഗ്രൂപ്പ് സമാംഗരൂപതയാണ്. അമൂർത്തമായ ഗ്രൂപ്പ് സംക്രിയയെ മാട്രിക്സ് ഗുണനമാക്കി മാറ്റുക വഴി ഗ്രൂപ്പിന്മേൽ മൂർത്തമായ കണക്കുകൂട്ടലുകൾ നടത്താൻ ഇത് സഹായിക്കുന്നു.

ഒരു ഗ്രൂപ്പിന്റെ ഗണിതവസ്തുവിനുമേലുള്ള പ്രവർത്തനം ആ ഗണിതവസ്തുവിനെക്കുറിച്ചും ഗ്രൂപ്പിനെക്കുറിച്ചും കൂടുതൽ കാര്യങ്ങൾ മനസ്സിലാക്കാൻ സഹായിക്കുന്നു. ലീ ഗ്രൂപ്പുകൾ, ബീജീയഗ്രൂപ്പുകൾ, സംസ്ഥിതീയഗ്രൂപ്പുകൾ മുതലായവയുടെ പഠനത്തിൽ പ്രാതിനിധ്യസിദ്ധാന്തം പ്രധാന പങ്കുവഹിക്കുന്നു.^[54]^[56]

ഗാൽവ ഗ്രൂപ്പുകൾ

ബഹുപദസമവാക്യങ്ങളുടെ സമമിതികളുപയോഗിച്ചുകൊണ്ട് അവയുടെ നിർദ്ധാരണം എളുപ്പമാക്കാൻ സഹായിക്കുന്ന ഗ്രൂപ്പുകളാണ് ഗാൽവ ഗ്രൂപ്പുകൾ.^[57]^[58] ഉദാഹരണമായി, ഫലകം:Nowrap beginax² + bx + c = 0ഫലകം:Nowrap end എന്ന ദ്വിമാനസമവാക്യത്തിന്റെ മൂലങ്ങൾ

x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} .

എന്നിവയാണ്. ഈ വ്യഞ്ജകത്തിൽ "+", "−" ചിഹ്നങ്ങൾ തമ്മിൽ പരസ്പരം മാറ്റുന്നത് മൂലങ്ങളുടെ ക്രമചയത്തിന് തുല്യമാണ്, ഇതിനെ ലളിതമായ ഒരു ഗ്രൂപ്പ് സംക്രിയയായി കണക്കാക്കാം. ഇതുപോലെ കൃതി മൂന്നും നാലുമുള്ള ബഹുപദസമവാക്യങ്ങളുടെയും മൂലങ്ങൾ കണ്ടുപിടിക്കാൻ സഹായിക്കുന്ന സൂത്രവാക്യങ്ങളുണ്ട്. എന്നാൽ അഞ്ചോ അധികമോ കൃതിയുള്ള ബഹുപദസമവാക്യങ്ങൾക്കൊന്നും നിർദ്ധാരണം കണ്ടുപിടിക്കാൻ പൊതുവായ സൂത്രവാക്യങ്ങളില്ല.^[59] ബഹുപദസമവാക്യങ്ങൾക്ക് ദ്വിമാനസമവാക്യത്തിലേതുപോലെ സങ്കലനം, വ്യവകലനം, മൂലങ്ങൾ എന്നിവ മാത്രമുപയോഗിച്ചുള്ള നിർദ്ധാരണങ്ങളുണ്ടോ എന്ന് ബന്ധപ്പെട്ട ഗാൽവ ഗ്രൂപ്പുകളുടെ സവിശേഷതകളുപയോഗിച്ച് കണ്ടുപിടിക്കാം.^[60]

പരിബദ്ധഗ്രൂപ്പുകൾ

അംഗങ്ങളുടെ എണ്ണം പരിബദ്ധമായുള്ള ഗ്രൂപ്പുകളാണ് പരിബദ്ധഗ്രൂപ്പുകൾ. ഗ്രൂപ്പിലെ അംഗങ്ങളുടെ എണ്ണത്തെ കോടി എന്ന് വിളിക്കുന്നു.^[61] N വസ്തുക്കളുടെ ക്രമചയങ്ങളുടെ ഗ്രൂപ്പായ സമമിതീയഗ്രൂപ്പ് S_N പരിബദ്ധഗ്രൂപ്പുകളുടെ ഒരു പ്രധാന വർഗ്ഗമാണ്. കെയ്ലി പ്രമേയമനുസരിച്ച് ഏതൊരു പരിബദ്ധഗ്രൂപ്പിനെയും ഒരു സമമിതീയഗ്രൂപ്പിന്റെ ഉപഗ്രൂപ്പായി എഴുതാൻ സാധിക്കും.

G എന്ന ഗ്രൂപ്പിലെ അംഗമാണ് a എന്നുണ്ടെങ്കിൽ aⁿ = e എന്ന സമവാക്യം ശരിയായി വരുന്ന ഏറ്റവും ചെറിയ ധനസംഖ്യയായ n നെ a യുടെ കോടി എന്ന് വിളിക്കുന്നു (• ഗ്രൂപ്പ് സംക്രിയയെ സൂചിപ്പിക്കുന്നുവെങ്കിൽ ഫലകം:Nowrap). G ഒരു പരിബദ്ധഗ്രൂപ്പാണെങ്കിൽ ഏതൊരംഗത്തിനും aⁿ = e സമവാക്യം ശരിയായിവരുന്ന ഒരു n ഉണ്ടായിരിക്കും, എന്നാൽ അനന്തഗ്രൂപ്പിലെ അംഗങ്ങൾക്ക് ഇങ്ങനെ ഉണ്ടായിക്കൊള്ളണമെന്നില്ല. a യുടെ കോടി a ജനകമായ ഉപഗ്രൂപ്പിന്റെ കോടിക്ക് തുല്യമാണ്.

സഹഗണങ്ങളുൾപ്പെടെയുള്ള ആശയങ്ങളുപയോഗിച്ചുള്ള കൂടുതൽ സങ്കീർണ്ണമായ എണ്ണൽ രിതികൾ പരിബദ്ധഗ്രൂപ്പുകളെക്കുറിച്ച് കൂടുതൽ മനസ്സിലാക്കാൻ സഹായിക്കുന്നു: ഏതൊരു ഗ്രൂപ്പിന്റെയും കോടി അതിന്റെ ഓരോ ഉപഗ്രൂപ്പിന്റെയും കോടിയുടെ ഗുണിതമായിരിക്കുമെന്ന് ലഗ്രാഞ്ച് പ്രമേയം പറയുന്നു. ഇതിന്റെ ഭാഗികവിപരിതമാണ് സൈലോ പ്രമേയങ്ങൾ.

മുകളിൽ വിവരിച്ച ഡൈഹെഡ്രൽ ഗ്രൂപ്പായ D₄ ൽ 8 അംഗങ്ങളാണുള്ളത്. ഗ്രൂപ്പിലെ അംഗമായ r₁ ന്റെയും അത് ജനകമായ R എന്ന ഉപഗ്രൂപ്പിന്റെയും കോടി 4 ആണ്. പ്രതിഫലന അംഗങ്ങളുടെയെല്ലാം കോടികൾ 2 ആണ്. ലഗ്രാഞ്ച് പ്രമേയം പ്രവചിക്കുന്നതുപോലെ ഈ കോടികളെല്ലാം ഗ്രൂപ്പ് കോടിയുടെ ഘടകങ്ങളാണെന്ന് കാണാം.

പരിബദ്ധ ലളിതഗ്രൂപ്പുകളുടെ വർഗ്ഗീകരണം

പരിബദ്ധ ലളിതഗ്രൂപ്പുകളുടെ വർഗ്ഗീകരണത്തിൽ പ്രധാന പങ്കു വഹിച്ച ഡാനിയൽ ഗോറൻസ്റ്റൈൻ

ഗണിതസങ്കല്പങ്ങളുടെ പൂർണ്ണമായ വർഗ്ഗീകരണം നടത്തി പട്ടികകളുണ്ടാക്കാൻ ഗണിതജ്ഞർ ശ്രമിക്കാറുണ്ട്. എന്നാൽ പരിബദ്ധഗ്രൂപ്പുകളെ ഇപ്രകാരം വർഗ്ഗീകരിക്കാൻ ശ്രമിക്കുന്നത് സങ്കീർണ്ണമായ ഗണിതത്തിലേക്ക് നയിക്കുന്നു. ലഗ്രാഞ്ച് പ്രമേയമനുസരിച്ച് കോടി p എന്ന അഭാജ്യസംഖ്യയായുള്ള ഗ്രൂപ്പുകളെല്ലാം ചാക്രികഗ്രൂപ്പുകളാണ് (Z_p). p² കോടിയുള്ള ഗ്രൂപ്പുകളൊക്കെ ക്രമഗ്രൂപ്പുകളാണെന്ന് തെളിയിക്കാനാകും, എന്നാൽ p³ കോടിയുള്ള ഗ്രൂപ്പുകൾ ക്രമമാകണമെന്നില്ല (ഡൈഹെഡ്രൽ ഗ്രൂപ്പായ D₄ ഉദാഹരണമാണ്).^[62] കമ്പ്യൂട്ടർ ആൾജിബ്ര സിസ്റ്റങ്ങളുപയോഗിച്ച് ചെറിയ ഗ്രൂപ്പുകളെയൊക്കെ പട്ടികപ്പെടുത്താനാകും, എന്നാൽ എല്ലാ പരിബദ്ധഗ്രൂപ്പുകളെയും ഇതുവരെ ഇങ്ങനെ വർഗ്ഗീകരിച്ച് പട്ടികപ്പെടുത്താൻ സാധിച്ചിട്ടില്ല.

എന്നിരുന്നാലും ഈ ദിശയിലേക്കുള്ള ഒരു പ്രധാന കാൽവെപ്പാണ് പരിബദ്ധ ലളിതഗ്രൂപ്പുകളുടെ വർഗ്ഗീകരണം. തുച്ഛമല്ലാത്ത ഒരു ഗ്രൂപ്പിന്റെ അഭിലംബ ഉപഗ്രൂപ്പുകൾ തുച്ഛ ഉപഗ്രൂപ്പും ആ ഗ്രൂപ്പു തന്നെയും ആണെങ്കിൽ ഗ്രൂപ്പിനെ ലളിതം എന്ന് വിളിക്കുന്നു. എല്ലാ പരിബദ്ധഗ്രൂപ്പുകളെയും നിർമ്മിച്ചിരിക്കുന്നത് പരിബദ്ധ ലളിതഗ്രൂപ്പുകൾ കൊണ്ടാണെന്ന് ജോർഡാൻ-ഹോൾഡർ പ്രമേയം പറയുന്നു.^[63] ആധുനിക ഗ്രൂപ്പ് സിദ്ധാന്തത്തിലെ ഒരു മുഖ്യമായ നേട്ടമായാണ് ഈ വർഗ്ഗീകരണത്തെ കണക്കാക്കുന്നത്. 1983-ൽ ഡാനിയൽ ഗോറൻസ്റ്റൈൻ ആണ് പരിബദ്ധ ലളിതഗ്രൂപ്പുകളെല്ലാം വർഗ്ഗീകരിക്കപ്പെട്ടതായി പ്രഖ്യാപിച്ചത്. എന്നാൽ quasithin ഗ്രൂപ്പുകളുടെ വർഗ്ഗീകരണത്തിന്റെ കാര്യം അദ്ദേഹം ശരിയായി മനസ്സിലാക്കിയിരുന്നില്ല. ഈ പ്രത്യേക ഗ്രൂപ്പിന്റെ കാര്യത്തിൽ തെളിവു കണ്ടുപിടിച്ച മൈക്കൽ ആഷ്ബാക്കർ ആണ് 2004-ൽ ലളിതഗ്രൂപ്പുകളുടെ വർഗ്ഗീകരണം പൂർത്തിയാക്കിയത്. പൂർണ്ണമായ വർഗ്ഗീകരണത്തിന്റെ തെളിവ് നൂറോളം ഗണിതജ്ഞരുടെ നൂറുകണക്കിന് ലേഖനങ്ങളിലായി പതിനായിരക്കണക്കിന് പേജൂകളെടുത്തു. 1998-ലെ ഫീൽഡ്സ് മെഡൽ ജേതാവായ റിച്ചാർഡ് ബോർച്ചെർഡ്സ് ഏറ്റവും വലിയ സ്പൊറാഡിക് ലളിതഗ്രൂപ്പായ മോൺസ്റ്റർ ഗ്രൂപ്പിന് മോഡ്യുലർ ഫലനങ്ങളുമായും ഭൗതികശാസ്ത്രത്തിലെ സ്ട്രിങ് തിയറിയുമായും ഉള്ള അടിസ്ഥാനപരമായ ബന്ധം തെളിയിച്ചു.^[64]

കൂടുതൽ ഘടനയുള്ള ഗ്രൂപ്പുകൾ

പല ഗ്രൂപ്പുകളും മറ്റ് ഗണിതഘടനകൾക്കും ഉദാഹരണങ്ങളാണ്. വർഗ്ഗസിദ്ധാന്തത്തിന്റെ ഭാഷയിൽ പറഞ്ഞാൽ, അവ ഒരു വർഗ്ഗത്തിലെ ഗ്രൂപ്പ് വസ്തുക്കളാണ്. അതായത്, അവ മറ്റൊരു ഗണിതഘടനയിലെ ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങൾക്ക് സമാനമായ പരിവർത്തനങ്ങളടങ്ങിയ വസ്തുക്കളാണ്. ഉദാഹരണമായി, ഏതൊരു ഗ്രൂപ്പും ഒരു ഗണം കൂടിയായതിനാൽ ഓരോ ഗ്രൂപ്പും ഗണങ്ങളുടെ വർഗ്ഗത്തിലെ ഒരു ഗ്രൂപ്പ് വസ്തുവാണ്.

സംസ്ഥിതീയഗ്രൂപ്പുകൾ

ചില സംസ്ഥിതീയസമഷ്ടികളിൽ ഗ്രൂപ്പ് സംക്രിയ നിർവചിക്കാനാവും. ഗ്രൂപ്പ് നിയമവും സംസ്ഥിതിയുടെ സവിശേഷതകളും ഒത്തുപോകണമെന്നുണ്ടെങ്കിൽ ഗ്രൂപ്പ് സംക്രിയകൾ സന്തതഫലനങ്ങളായിരിക്കണം. അതായത് g, h എന്നിവ അല്പം മാത്രമേ മാറുന്നുള്ളൂ എങ്കിൽ ഫലകം:Nowrap g⁻¹ എന്നിവയും അല്പമേ മാറാൻ പാടുള്ളൂ. ഇത്തരം ഗ്രൂപ്പുകളെ സംസ്ഥിതീയഗ്രൂപ്പുകൾ എന്ന് വിളിക്കുന്നു. സംസ്ഥിതീയസമഷ്ടികളുടെ വർഗ്ഗത്തിലെ ഗ്രൂപ്പ് വസ്തുക്കളാണിവ. ^[65] സങ്കലനം സംക്രിയയായ വാസ്തവികസംഖ്യകളുടെ ഗ്രൂപ്പ് ഫലകം:Nowrap, ഗുണനം സംക്രിയയായ അശൂന്യ വാസ്തവികസംഖ്യകളുടെ ഗ്രൂപ്പ് ഫലകം:Nowrap തുടങ്ങിയവ ഉദാഹരണങ്ങളാണ്. ഈ ഗ്രൂപ്പുകളെല്ലാം തദ്ദേശീയമായി സാന്ദ്രമായതിനാൽ (locally compact) അവയ്ക്ക് ഹാർ അളവുകളുണ്ട്, അവയെ ഹാർമോണിക് അനാലിസിസ് വഴി പഠിക്കാനാകും.

ഈ ക്ഷേത്രങ്ങൾക്കു മേലുള്ള മാട്രിക്സ് ഗ്രൂപ്പുകളും സംഖ്യാസിദ്ധാന്തത്തിലെ അഡെൽ വലയങ്ങളും അഡെൽ ബീജീയഗ്രൂപ്പുകളും മറ്റ് ഉദാഹരണങ്ങളാണ്.^[66] അനന്തക്ഷേത്രങ്ങളുടെ വിപുലീകരണങ്ങളുടെ ഗാൽവ ഗ്രൂപ്പുകൾക്കുമേലും (കേവല ഗാൽവ ഗ്രൂപ്പ് ഉദാഹരണമാണ്) ക്രൾ സംസ്ഥിതി എന്ന സംസ്ഥിതി ചേർക്കാനാകും.^[67] ബീജീയജ്യാമിതിയുടെ ആവശ്യങ്ങൾക്കായി ഈ ആശയത്തിന്റെ സാമാന്യവൽക്കരണമാണ് എറ്റാലെ അടിസ്ഥാനഗ്രൂപ്പ്.^[68]

ലീ ഗ്രൂപ്പുകൾ

മെനിഫോൾഡ് ഘടനയുള്ള ഗ്രൂപ്പുകളാണ് ലീ ഗ്രൂപ്പുകൾ. അതായത്, തദ്ദേശീയമായി അവ ഏതെങ്കിലും മാനമുള്ള യൂക്ലിഡിയൻ സമഷ്ടിക്ക് സമാനമായിരിക്കും.^[69] നോർവീജിയൻ ഗണിതജ്ഞനായ സോഫസ് ലീയുടെ ബഹുമാനാർഥമാണ് ഈ നാമകരണം. ഇവിടെയും മെനിഫോൾഡ് ഘടന ഗ്രൂപ്പ് സ്വയംപ്രമാണങ്ങളുമായി ഒത്തുപോവണമെങ്കിൽ ഗുണനവും വിപരീതവും smooth ഫലനങ്ങളായിരിക്കണം. മേൽ വിവരിച്ച സാമാന്യ രേഖീയഗ്രൂപ്പ് n×n മാട്രിക്സുകളുടെ സമഷ്ടിയുടെ തുറന്ന ഉപഗണമായതിനാൽ ഒരു ലീ ഗ്രൂപ്പാണ്.^[70]

ലീ ഗ്രൂപ്പുകൾ ആധുനിക ഭൗതികശാസ്ത്രത്തിൽ വളരെ പ്രാധാന്യമുള്ളവയാണ്. സന്തതസമമിതികളെ നോയ്തർ സിദ്ധാന്തം ഭൗതികശാസ്ത്രത്തിലെ സംരക്ഷിതപരിമാണങ്ങളുമായി ബന്ധപ്പെടുത്തുന്നു. പരിക്രമണം, സ്ഥലത്തിലും കാലത്തിലുമുള്ള നീക്കൽ (translation) എന്നിവ ബലതന്ത്രത്തിലെ അടിസ്ഥാനപരമായ സന്തതസമമിതികളാണ്. ഇവ യഥാക്രമം കോണീയസംവേഗം, രേഖീയസംവേഗം, ഊർജ്ജം എന്നിവയുടെ സംരക്ഷണവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു. ആപേക്ഷികമായി ചലിച്ചുകൊണ്ടിരിക്കുന്ന രണ്ട് നിരീക്ഷകരുടെ സ്ഥലകാല അളവുകളെ തമ്മിൽ ബന്ധപ്പെടുത്തുന്ന ലോറെന്റ്സ് പരിവർത്തനം മറ്റൊരുദാഹരണമാണ്. മിങ്കോവ്സ്കി സമഷ്ടിയിലെ പരിക്രമണസമമിതിയായി ഇതിന്റെ കണ്ട് തികച്ചും ഗ്രൂപ്പ് സിദ്ധാന്തരിതിയിൽ ഈ പരിവർത്തനങ്ങൾ കണ്ടെത്താവുന്നതാണ്. സാമാന്യ ആപേക്ഷികതാസിദ്ധാന്തത്തിൽ സ്ഥലകാലത്തിന്റെ മാതൃകയാണിത്.^[71] നീക്കലുകലും കൂടി ഉൾപ്പെടുത്തിയാൽ മിങ്കോവ്സ്കി സമഷ്ടിയിലെ സമമിതികളുടെ ഗ്രൂപ്പ് പോങ്കാരെ ഗ്രൂപ്പ് എന്നറിയപ്പെടുന്നു. ഇതിന് സാമാന്യ ആപേക്ഷികതയിലും ക്വാണ്ടം ഫീൽഡ് സിദ്ധാന്തത്തിലും ഉപയോഗമുണ്ട്.^[72] ഗേജ് സിദ്ധാന്തത്തിന്റെ സഹായത്തോടെ ഭൗതികശാസ്ത്രത്തിലെ പ്രതിപ്രവർത്തനങ്ങളെ വിശദീകരിക്കുന്നതിൽ തദ്ദേശീയസമമിതികൾക്ക് കേന്ദ്രസ്ഥാനമുണ്ട്.^[73]

അവലംബം

ഫലകം:Reflist

ഗ്രന്ഥസൂചി

ഗ്രൂപ്പ്

ഉള്ളടക്കം

ഉദാഹരണങ്ങൾ

ആദ്യത്തെ ഉദാഹരണം : പൂർണ്ണസംഖ്യകൾ

ഗ്രൂപ്പ് : നിർവചനം

രണ്ടാമത്തെ ഉദാഹരണം : ഒരു സമമിതിഗ്രൂപ്പ്

ചരിത്രം

പ്രാഥമിക ഗ്രൂപ്പ് സിദ്ധാന്തം

തൽസമകവും വിപരിതങ്ങളും അദ്വിതീയമാണ്

ഹരണം

അടിസ്ഥാന ആശയങ്ങൾ

ഗ്രൂപ്പ് സമാംഗരൂപത

ഉപഗ്രൂപ്പ്

സഹഗണം

ഘടകഗ്രൂപ്പുകൾ

ഉദാഹരണങ്ങളും പ്രയോഗങ്ങളും

സംഖ്യകൾ

പൂർണ്ണസംഖ്യകൾ

ഭിന്നകങ്ങൾ

പൂർണ്ണസംഖ്യകളുടെ മോഡ്യുലോ അഭാജ്യസംഖ്യയായുള്ള ഗ്രൂപ്പ്

ചാക്രികഗ്രൂപ്പുകൾ

ക്രമഗ്രൂപ്പുകൾ

സമമിതിഗ്രൂപ്പുകൾ

സാമാന്യ രേഖീയഗ്രൂപ്പും പ്രാതിനിധ്യസിദ്ധാന്തവും

ഗാൽവ ഗ്രൂപ്പുകൾ

പരിബദ്ധഗ്രൂപ്പുകൾ

പരിബദ്ധ ലളിതഗ്രൂപ്പുകളുടെ വർഗ്ഗീകരണം

കൂടുതൽ ഘടനയുള്ള ഗ്രൂപ്പുകൾ

സംസ്ഥിതീയഗ്രൂപ്പുകൾ

ലീ ഗ്രൂപ്പുകൾ

അവലംബം

ഗ്രന്ഥസൂചി

പൊതുവായ അവലംബങ്ങൾ

പ്രത്യേക അവലംബങ്ങൾ

ചരിത്രപരമായ അവലംബങ്ങൾ

ഗമന വഴികാട്ടി

(f_d • f_v) • r₂	=	r₃ • r₂	=	r₁, ഇത്
f_d • (f_v • r₂)	=	f_d • f_h	=	r₁ എന്നതിന് തുല്യമാണ്.

ഗ്രൂപ്പ്

ഉദാഹരണങ്ങൾ

ആദ്യത്തെ ഉദാഹരണം : പൂർണ്ണസംഖ്യകൾ

ഗ്രൂപ്പ് : നിർവചനം

രണ്ടാമത്തെ ഉദാഹരണം : ഒരു സമമിതിഗ്രൂപ്പ്

ചരിത്രം

പ്രാഥമിക ഗ്രൂപ്പ് സിദ്ധാന്തം

തൽസമകവും വിപരിതങ്ങളും അദ്വിതീയമാണ്

ഹരണം

അടിസ്ഥാന ആശയങ്ങൾ

ഗ്രൂപ്പ് സമാംഗരൂപത

ഉപഗ്രൂപ്പ്

സഹഗണം

ഘടകഗ്രൂപ്പുകൾ

ഉദാഹരണങ്ങളും പ്രയോഗങ്ങളും

സംഖ്യകൾ

പൂർണ്ണസംഖ്യകൾ

ഭിന്നകങ്ങൾ

പൂർണ്ണസംഖ്യകളുടെ മോഡ്യുലോ അഭാജ്യസംഖ്യയായുള്ള ഗ്രൂപ്പ്

ചാക്രികഗ്രൂപ്പുകൾ

ക്രമഗ്രൂപ്പുകൾ

സമമിതിഗ്രൂപ്പുകൾ

സാമാന്യ രേഖീയഗ്രൂപ്പും പ്രാതിനിധ്യസിദ്ധാന്തവും

ഗാൽവ ഗ്രൂപ്പുകൾ

പരിബദ്ധഗ്രൂപ്പുകൾ

പരിബദ്ധ ലളിതഗ്രൂപ്പുകളുടെ വർഗ്ഗീകരണം

കൂടുതൽ ഘടനയുള്ള ഗ്രൂപ്പുകൾ

സംസ്ഥിതീയഗ്രൂപ്പുകൾ

ലീ ഗ്രൂപ്പുകൾ

അവലംബം

ഗ്രന്ഥസൂചി

പൊതുവായ അവലംബങ്ങൾ

പ്രത്യേക അവലംബങ്ങൾ

ചരിത്രപരമായ അവലംബങ്ങൾ

ഗമന വഴികാട്ടി

തിരയൂ